题目内容
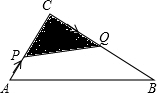 已知:如图,△ABC中,∠C=90°,AC=3厘米,CB=4厘米.两个动点P、Q分别从A、C两点同时按顺时针方向沿△ABC的边运动.当点Q运动到点A时,P、Q两点运动即停止.点P、Q的运动速度分别为1厘米/秒、2厘米/秒,设点P运动时间为t(秒).
已知:如图,△ABC中,∠C=90°,AC=3厘米,CB=4厘米.两个动点P、Q分别从A、C两点同时按顺时针方向沿△ABC的边运动.当点Q运动到点A时,P、Q两点运动即停止.点P、Q的运动速度分别为1厘米/秒、2厘米/秒,设点P运动时间为t(秒).(1)当时间t为何值时,以P、C、Q三点为顶点的三角形的面积(图中的阴影部分)等于2厘米2;
(2)当点P、Q运动时,阴影部分的形状随之变化.设PQ与△ABC围成阴影部分面积为S(厘米2),求出S与时间t的函数关系式,并指出自变量t的取值范围;
(3)点P、Q在运动的过程中,阴影部分面积S有最大值吗?若有,请求出最大值;若没有,请说明理由.
分析:(1)由于PC=3-t,CQ=2t,∠C=90°,可表示S△PCQ,从而求出t的值;
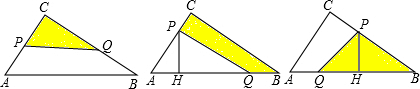
(2)根据运动状态,分三种可能情况:①当0<t≤2时,②当2<t≤3时,③当3<t≤4.5时,分别表示阴影部分面积,在②中,S=S△ABC-S△APQ,由,∠C=90°,AC=3厘米,CB=4厘米,用勾股定理可求AB=5厘米,作PH⊥AB于H,利用相似比表示PH,再表示面积;
(3)用(2)的结论,分别求出每一种情况下的最大值(注意自变量取值范围),再比较,求出整个过程中的最大值.
(2)根据运动状态,分三种可能情况:①当0<t≤2时,②当2<t≤3时,③当3<t≤4.5时,分别表示阴影部分面积,在②中,S=S△ABC-S△APQ,由,∠C=90°,AC=3厘米,CB=4厘米,用勾股定理可求AB=5厘米,作PH⊥AB于H,利用相似比表示PH,再表示面积;
(3)用(2)的结论,分别求出每一种情况下的最大值(注意自变量取值范围),再比较,求出整个过程中的最大值.
解答:解:(1)
S△PCQ=
PC•CQ=
(3-t)•2t=(3-t)t=2,
解得t1=1,t2=2.
∴当时间t为1秒或2秒时,S△PCQ=2厘米2;
(2)①当0<t≤2时,S△PCQ=
PC•CQ=
(3-t)•2t=(3-t)t,S=-t2+3t;
②当2<t≤3时,AQ=9-2t,
作PH⊥AB于H,则△AHP∽△ACB,
∴PH:BC=AP:AB
∴PH=
t,
∴S=S△ABC-S△APQ,即S=
t2-
t+6;
③在3<t≤4.5时,CP=t-AC=t-3,则BP=BC-PC=4-(t-3)=7-t,
∵△ABC∽△PBH,
∴
=
,即
=
,
故PH=
,
又∵BQ=2t-BC=2t-4,
∴S=
BQ•PH=
(2t-4)•
=-
t2+
t-
;
(3)有最大值.
①在0<t≤2时,S=-t2+3t=-(t-
)2+
,当t=
,S有最大值,S1=
;
②在2<t≤3时,S=
t2-
t+6=
(t-
)2+
,当t=
,S有最大值,S2=
;
③在3<t≤4.5时,S=-
t2+
t-
=-
(t-
)2+
,当t=
,S有最大值,S3=
;
∵S2<S1<S3
∴t=
时,S有最大值,S最大值=
.
S△PCQ=
| 1 |
| 2 |
| 1 |
| 2 |
解得t1=1,t2=2.
∴当时间t为1秒或2秒时,S△PCQ=2厘米2;
(2)①当0<t≤2时,S△PCQ=
| 1 |
| 2 |
| 1 |
| 2 |
②当2<t≤3时,AQ=9-2t,
作PH⊥AB于H,则△AHP∽△ACB,
∴PH:BC=AP:AB
∴PH=
| 4 |
| 5 |
∴S=S△ABC-S△APQ,即S=
| 4 |
| 5 |
| 18 |
| 5 |
③在3<t≤4.5时,CP=t-AC=t-3,则BP=BC-PC=4-(t-3)=7-t,
∵△ABC∽△PBH,
∴
| PH |
| AC |
| BP |
| AB |
| PH |
| 3 |
| 7-t |
| 5 |
故PH=
| 21-3t |
| 5 |
又∵BQ=2t-BC=2t-4,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 21-3t |
| 5 |
| 3 |
| 5 |
| 27 |
| 5 |
| 42 |
| 5 |

(3)有最大值.
①在0<t≤2时,S=-t2+3t=-(t-
| 3 |
| 2 |
| 9 |
| 4 |
| 3 |
| 2 |
| 9 |
| 4 |
②在2<t≤3时,S=
| 4 |
| 5 |
| 18 |
| 5 |
| 4 |
| 5 |
| 9 |
| 4 |
| 39 |
| 20 |
| 9 |
| 4 |
| 39 |
| 20 |
③在3<t≤4.5时,S=-
| 3 |
| 5 |
| 27 |
| 5 |
| 42 |
| 5 |
| 3 |
| 5 |
| 9 |
| 2 |
| 15 |
| 4 |
| 9 |
| 2 |
| 15 |
| 4 |
∵S2<S1<S3
∴t=
| 9 |
| 2 |
| 15 |
| 4 |
点评:本题考查了二次函数的实际运用,以时间t为自变量,面积为函数,形成二次函数关系式,再求二次函数最大值;同时,渗透了分类讨论的思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N.
17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N. 已知:如图,∠ABC、∠ACB 的平分线相交于点F,过F作DE∥BC于D,交AC 于E,且AB=6,AC=5,求三角形ADE的周长.
已知:如图,∠ABC、∠ACB 的平分线相交于点F,过F作DE∥BC于D,交AC 于E,且AB=6,AC=5,求三角形ADE的周长. 已知:如图,△ABC是等边三角形,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:BF=CF+CE.
已知:如图,△ABC是等边三角形,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:BF=CF+CE. 已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A.
已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A. 已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.
已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.