题目内容
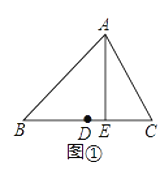
【题目】如图,△ABC中,∠ABC=30°,点D在△ABC外,且BD=2.连AD、CD,则△ACD的周长最小值为( )

A. 1B. ![]() C. 2D. 2
C. 2D. 2![]()
【答案】C
【解析】
作D关于直线BA的对称点M,直线BC的对称点N,根据图形对称的性质,可得线段MN的长度即为△ACD的周长的最小值,再结合已知条件可证△MBN是等边三角形,MN=2.
解:作D关于直线BA的对称点M,直线BC的对称点N,连接MN,则线段MN的长度即为△ACD的周长的最小值,
由对称的性质得到∠MBA=∠DBA,∠NBD=∠DBC,BM=BD=BN,
∴∠MBA+∠NBC=∠ABC=30°,
∴∠MBN=60°,
∴△MBN是等边三角形,
∴MN=BM=BD=2,
∴△ACD的周长最小值为2,
故选:C.


练习册系列答案
相关题目
【题目】沾益区兴隆水果店计划用1000元购进甲、乙两种新出产的水果140千克,这两种水果的进价、售价如下表所示:
进价(元/千克) | 售价(元/千克) | |
甲 | 5 | 8 |
乙 | 9 | 13 |
(1)这两种水果各购进多少千克?
(2)该水果店全部销售完这批水果时获利多少元?