题目内容
 将连续的奇数1,3,5,7,…排成如下数字表,用十子框框出5个数,如图所示.
将连续的奇数1,3,5,7,…排成如下数字表,用十子框框出5个数,如图所示.(1)如果十字框图中横排3个数之和为51,那么竖列的3个数之和为
51
51
,竖列的3个数最下面一个数是29
29
(2)若十字框框住的5个数中中间那个数为n,则a+b+c+d+e=
5n
5n
.分析:(1)设横排第一个数为x,后面的依次为x+2,x+4,利用十字框图中横排3个数之和为51列出关于x的方程,求出方程的解得到x的值,确定出中间的数字为17,由图形可得出上面与下面的数字,得到竖列的3个数之和;
(2)由十字框框住的5个数中间为n,得到c=n,根据图形中数字规律表示出a,b,d,e,代入a+b+c+d+e中化简,即可得到结果.
(2)由十字框框住的5个数中间为n,得到c=n,根据图形中数字规律表示出a,b,d,e,代入a+b+c+d+e中化简,即可得到结果.
解答:解:(1)设横排第一个数为x,后面的依次为x+2,x+4,
根据题意列得:x+x+2+x+4=51,
解得:x=15,
∴横排的三个数分别为15,17,19,
∴竖排三个数分别为5,17,29,
则竖列三个数之和为5+17+29=51;
(2)由5个数中中间的数为n,即c=n,
得到前一个数b=n-2,后一个d=n+2,上边的数a=n-12,下边的数e=n+12,
则a+b+c+d+e=n-12+n-2+n+n+2+n+12=5n.
故答案为:(1)51;29;(2)5n
根据题意列得:x+x+2+x+4=51,
解得:x=15,
∴横排的三个数分别为15,17,19,
∴竖排三个数分别为5,17,29,
则竖列三个数之和为5+17+29=51;
(2)由5个数中中间的数为n,即c=n,
得到前一个数b=n-2,后一个d=n+2,上边的数a=n-12,下边的数e=n+12,
则a+b+c+d+e=n-12+n-2+n+n+2+n+12=5n.
故答案为:(1)51;29;(2)5n
点评:此题考查了规律型:数字的变化类,观察图形得出其中的规律是解本题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
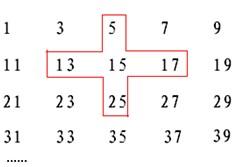
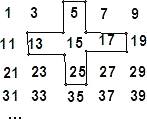 将连续的奇数1,3,5,7,9…,排成如图的数表,问:
将连续的奇数1,3,5,7,9…,排成如图的数表,问: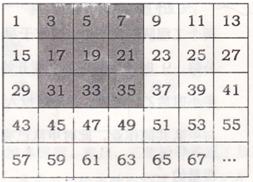
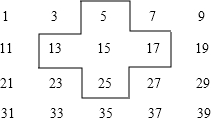 将连续的奇数1,3,5,7,9…排成如图的数表:
将连续的奇数1,3,5,7,9…排成如图的数表: