题目内容
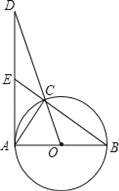
【题目】如图,已知AB是⊙O的直径,点C为圆上一点,点D在OC的延长线上,连接DA,
交BC的延长线于点E,使得∠DAC=∠B.
(1)求证:DA是⊙O切线;
(2)求证:△CED∽△ACD;
(3)若OA=1,sinD=![]() ,求AE的长.
,求AE的长.
【答案】(1)证明见解析;(2)![]()
【解析】分析:(1)由圆周角定理和已知条件求出AD⊥AB即可证明DA是⊙O切线;
(2)由∠DAC=∠DCE,∠D=∠D可知△DEC∽△DCA;
(3)由题意可知AO=1,OD=3,DC=2,由勾股定理可知AD=2,故此可得到DC2=DEAD,故此可求得DE的长,于是可求得AE的长.
详解:(1)∵AB为⊙O的直径,∴∠ACB=90°,∴∠CAB+∠B=90°.
∵∠DAC=∠B,∴∠CAB+∠DAC=90°,∴AD⊥AB.
∵OA是⊙O半径,∴DA为⊙O的切线;
(2)∵OB=OC,∴∠OCB=∠B.
∵∠DCE=∠OCB,∴∠DCE=∠B.
∵∠DAC=∠B,∴∠DAC=∠DCE.
∵∠D=∠D,∴△CED∽△ACD;
(3)在Rt△AOD中,OA=1,sinD=![]() ,∴OD=
,∴OD=![]() =3,∴CD=OD﹣OC=2.
=3,∴CD=OD﹣OC=2.
∵AD=![]() =2
=2![]() .
.
又∵△CED∽△ACD,∴![]() ,∴DE=
,∴DE=![]() =
=![]() ,
,
∴AE=AD﹣DE=2![]() ﹣
﹣![]() =
=![]() .
.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案【题目】新个税法于2018年9月1日全面实施,工资、薪金所得基本减除费用标准由3500元提高至5000元,并按新的税率表计算纳税:
序号 | 税前每月工资的各部分 | 税率 |
1 | 不超过5000元部分 | 0% |
2 | 超过5000元至8000元的部分 | 3% |
3 | 超过8000元至17000元的部分 | 10% |
4 | 超过17000元至30000元的部分 | 20% |
5 | 超过30000元至40000元的部分 | 25% |
6 | 超过40000元至60000元的部分 | 30% |
7 | 超过60000元至80000元的部分 | 35% |
8 | 超过80000元的部分 | 45% |
(1)在新个税法实施后,小王没扣税前某月工资7800元,他这个月应交税 元;
(2)在新个税法实施后,若小李没扣税前某月工资x元![]() ,他这个月交税y元,则y= ;
,他这个月交税y元,则y= ;
(3)在新个税法实施后,一企业某月把奖金放在工资里发放(奖金跟工资一起扣税),该企业员工小刘这个月领取了工资加奖金(税后)26410元.已知小刘没扣税前工资为a元![]() ,若工资和奖金分两次发放(工资扣税,奖金不扣税),小刘这个月可以领取多少钱?(如需要,可用含a 的代数式表示)
,若工资和奖金分两次发放(工资扣税,奖金不扣税),小刘这个月可以领取多少钱?(如需要,可用含a 的代数式表示)