题目内容
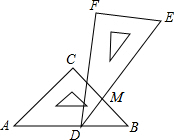 如图,一副三角板叠在一起如图所示放置,最小锐角的点D恰好放在等腰直角三角板的斜边AB上,BC与DE交于点M,如果∠ADF=100°,那么∠BME为
如图,一副三角板叠在一起如图所示放置,最小锐角的点D恰好放在等腰直角三角板的斜边AB上,BC与DE交于点M,如果∠ADF=100°,那么∠BME为考点:三角形的外角性质
专题:计算题
分析:先求出∠BDM,再根据三角形的外角性质求出即可.
解答:解:∵∠BDM=180°-∠ADF-∠FDE=180°-100°-30°=50°,∠B=45°,
∴∠BME=∠B+∠BDM=45°+50°=95°,
故答案为:95.
∴∠BME=∠B+∠BDM=45°+50°=95°,
故答案为:95.
点评:本题考查了三角形的外角性质的应用,注意:三角形的一个外角等于和它不相邻的两个内角的和.

练习册系列答案
相关题目
下列命题中是假命题的是( )
| A、若a>b,则ac>bc | ||
| B、垂直于弦的直径平分弦 | ||
| C、对角线互相平分且垂直的四边形是菱形 | ||
D、反比例函数y=
|