题目内容
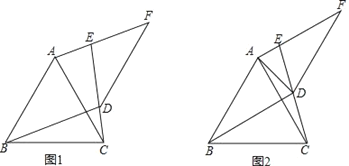
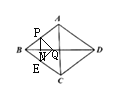
【题目】如图,在菱形![]() 中,对角线
中,对角线![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向匀速运动,速度是
方向匀速运动,速度是![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向匀速运动,速度是
方向匀速运动,速度是![]() ,
,![]() ,与
,与![]() 交于点
交于点![]() ,连接
,连接![]() .设运动时间为
.设运动时间为![]() .
.
(1)当![]() 于
于![]() 时,求
时,求![]() 的值;
的值;
(2)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)是否存在某一时刻![]() ,使
,使![]() 平分
平分![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
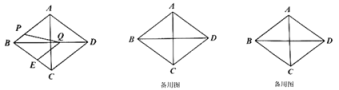
【答案】(1)当![]() 时
时![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时
时![]() 平分
平分![]() .
.
【解析】
(1)由题意得:![]() ,
,![]() ,
,![]() ,根据菱形的性质求出AO、BO、AB的值,再根据同角的余弦得出cos∠ABO
,根据菱形的性质求出AO、BO、AB的值,再根据同角的余弦得出cos∠ABO![]() ,代入计算即可求解;
,代入计算即可求解;
(2)过![]() 作
作![]() ,垂足为
,垂足为![]() ,根据同角的正弦弦得出sin∠ABO
,根据同角的正弦弦得出sin∠ABO![]() ,求出MQ,根据平行证出
,求出MQ,根据平行证出![]() ,由相似三角形的性质求出EQ,根据梯形的面积公式即可求得
,由相似三角形的性质求出EQ,根据梯形的面积公式即可求得![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)假设存在时刻![]() ,使
,使![]() 平分
平分![]() ,则
,则![]() ,过
,过![]() 作
作![]() ,垂足为
,垂足为![]() ,先证出△PBQ是等腰三角形,根据三线合一可得BN=
,先证出△PBQ是等腰三角形,根据三线合一可得BN=![]() BQ=4-t,再根据同角的余弦得出cos∠ABO
BQ=4-t,再根据同角的余弦得出cos∠ABO![]() ,代入计算即可求
,代入计算即可求![]() 的值.
的值.
解:(1)由题意得:![]() ,
,![]() ,
,![]() .
.
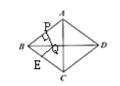
∵四边形![]() 是菱形,
是菱形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
假设存在![]() 使
使![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() ,
,
得![]() .
.
∴当![]() 时
时![]() ;
;
(2)过![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
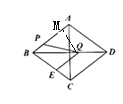
在![]() 中,
中,
![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,四边形BPQE是梯形,
,四边形BPQE是梯形,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)假设存在时刻![]() ,使
,使![]() 平分
平分![]() ,则
,则![]() ,
,
过![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() ,
,
解得![]() .
.
∴当![]() 时
时![]() 平分
平分![]() .
.
故答案为:(1)当![]() 时
时![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时
时![]() 平分
平分![]() .
.

练习册系列答案
相关题目