题目内容
6.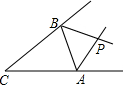 如图,△ABC的∠ABC的外角的平分线BD与∠ACB的外角的平分线CE相交于P.求证:点P到三边AB,BC,CA所在的直线的距离相等.
如图,△ABC的∠ABC的外角的平分线BD与∠ACB的外角的平分线CE相交于P.求证:点P到三边AB,BC,CA所在的直线的距离相等.
分析 过点P作PF⊥BC于F,PG⊥AB于G,PH⊥AC于H,然后根据角平分线上的点到角的两边的距离相等可得PF=PG=PH.
解答 证明:如图,过点P作PF⊥BC于F,PG⊥AB于G,PH⊥AC于H,
∵△ABC的∠ABC的外角的平分线BD与∠ACB的外角的平分线CE相交于P,
∴PF=PG,PG=PH,
∴PF=PG=PH,
∴点P到三边AB、BC、CA所在直线的距离相等.
点评 本题考查了角平分线的性质,掌握角平分线上的点到角的两边的距离相等的性质熟记性质是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
17.上海是世界知名金融中心,以下能准确表示上海市地理位置的是( )
| A. | 在中国的东南方 | B. | 东经121.5° | ||
| C. | 在中国的长江出海口 | D. | 东经121°29′,北纬31°14′ |
18.下列各对数中,互为相反数的是( )
| A. | -|-7|和+(-7) | B. | +(-10)和-(+10) | C. | (-4)3和-43 | D. | (-2)4和-24 |
15.一辆汽车在n秒内行驶m米,按此速度它在2分钟内可行驶( )米.
| A. | $\frac{m}{2n}$ | B. | $\frac{2m}{n}$ | C. | $\frac{120m}{n}$ | D. | $\frac{m}{120n}$ |
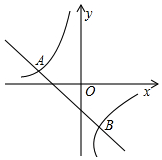 如图,已知一次函数与反比例函数y=$\frac{k}{x}$的图象相交于点 A(-3,1)和点B(a,-3)
如图,已知一次函数与反比例函数y=$\frac{k}{x}$的图象相交于点 A(-3,1)和点B(a,-3)