Question

【题目】如图，在△ABC中，AB＝AC，点P是边BC上的中点，PD⊥AB，PE⊥AC，垂足分别为点D、E．

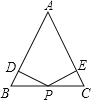
（1）求证：PD＝PE；

（2）若AB＝6cm，∠BAC＝30°，请直接写出PD+PE＝　 　cm．

Answer 1

【答案】（1）见解析；（2）3

【解析】

（1）根据等腰三角形性质可知，再由“AAS”可证△PDB≌△PEC，可得PD＝PE；

（2）由直角三角形的性质可得CH＝3cm，由S△ABC＝S△ABP+S△ACP，可求解．

解：（1）∵AB＝AC，

∴∠B＝∠C，

∵点P是边BC上的中点，

∴PB＝PC，且∠B＝∠C，∠PDB＝∠PEC＝90°，

∴△PDB≌△PEC(AAS)

∴PD＝PE；

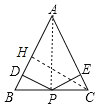
（2）过点C作于H，连接AP，

，，

，

，

，

故答案为：3．