题目内容
【题目】已知:如图,在△ABC中,∠ABC=45°,AH⊥BC于点H,点D为AH上的一点,且DH=HC,连接BD并延长BD交AC于点E,连接EH.
(1)请补全图形;
(2)求证:△ABE是直角三角形;
(3)若BE=a,CE=b,求出S△CEH:S△BEH的值(用含有a,b的代数式表示)

【答案】(1)见解析;(2)证明见解析;(3)![]() ;
;
【解析】
(1)根据题意直接补全图形;
(2)证明△BHD≌△AHC,根据全等三角形的性质,得到∠HBD=∠CAH,又∠HBD+∠BDH=90°,∠BDH=∠ADE,即可得到∠ADE+∠DAE=90°,根据三角形的内角和得到∠AED=90°,即可证明△ABE是直角三角形;
(3)作HM⊥BE于M,HN⊥AC于N.根据全等三角形的性质得到HM=HN,根据三角形的面积公式即可求出S△CEH:S△BEH的值.
(1)解:图形如图所示;
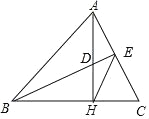
(2)证明:∵AH⊥BC,
∴∠BHD=∠AEH=90°,
∵∠ABC=45°,
∴∠BAH=∠ABH=45°,
∴AH=BH,
在△BHD和△AHC中,
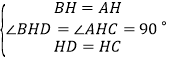
∴△BHD≌△AHC(SAS),
∴∠HBD=∠CAH,
∵∠HBD+∠BDH=90°,∠BDH=∠ADE,
∴∠ADE+∠DAE=90°,
∴∠AED=90°,
∴△ABE是直角三角形.
(3)作HM⊥BE于M,HN⊥AC于N.
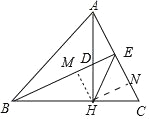
∵△BHD≌△AHC,
∴HM=HN(全等三角形对应边上的高相等),
∴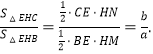

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目