题目内容
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(![]() )天的售价与销量的相关信息如下表:
)天的售价与销量的相关信息如下表:
时间(天) |
|
|
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | 200-2x |
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大?最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
【答案】(1)y=![]() ,(2) 第45天时,最大利润为6050元;(3)41天.
,(2) 第45天时,最大利润为6050元;(3)41天.
【解析】(1)根据单价乘以数量,可得利润,即可得出答案;
(2)分别求出两段函数的最大值,再比较即可;
(3)根据二次函数值大于或等于4800,一次函数值大于或等于4800,可得不等式组,根据解不等式组,可得答案.
解:(1)当1≤x<50时,y=(200-2x)(x+40-30)=-2x2+180x+2000,
当50≤x≤90时,
y=(200-2x)(90-30)=-120x+12000,
综上所述:
y=![]() ,
,
(2)当1≤x<50时,
y=-2x2+180x+2000,
y=-2(x-45)2+6050.
∴a=-2<0,
∴二次函数开口下,二次函数对称轴为x=45,
当x=45时,y最大=6050,
当50≤x≤90时,y随x的增大而减小,
当x=50时,y最大=6000,
综上所述,该商品第45天时,当天销售利润最大,最大利润是6050元;
(3)①当1≤x<50时,y=-2x2+180x+2000≥4800,
解得:20≤x<70,
因此利润不低于4800元的天数是20≤x<50,共30天;
②当50≤x≤90时,y=-120x+12000≥4800,
解得:x≤60,
因此利润不低于4800元的天数是50≤x≤60,共11天,
所以该商品在整个销售过程中,共41天每天销售利润不低于4800元.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案【题目】为了提高学生书写汉字的能力,增强保护汉字的意识,某市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如下:
组别 | 成绩x分 | 频数(人数) |
第1组 | 25≤x<30 | 4 |
第2组 | 30≤x<35 | 8 |
第3组 | 35≤x<40 | 16 |
第4组 | 40≤x<45 | a |
第5组 | 45≤x<50 | 10 |
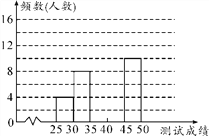
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
(4)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小宇与小强两名男同学能分在同一组的概率.