题目内容
盼盼同学在学习正多边形时,发现了以下一组有趣的结论:
①若P是圆内接正三角形ABC的外接圆的
 上一点,则PB+PC=PA;
上一点,则PB+PC=PA;②若P是圆内接正四边形ABCD的外接圆的
 上一点,则
上一点,则 ;
;③若P是圆内接正五边形ABCDE的外接圆的
 上一点,请问PB+PE与PA有怎样的数量关系,写出结论,并加以证明;
上一点,请问PB+PE与PA有怎样的数量关系,写出结论,并加以证明;④若P是圆内接正n边形A1A2A3…An的外接圆的
 上一点,请问PA2+PAn与PA1又有怎样的数量关系,写出结论,不要求证明.
上一点,请问PA2+PAn与PA1又有怎样的数量关系,写出结论,不要求证明.
【答案】分析:PB+PC=PA,可以在PA上截取一条线段等于PB,然后证明剩下的部分等于PC即可,其它三问的解决思路相同.
解答:解:
③PB+PE与PA满足的数量关系是:PB+PE=2PA•cos36°;(3分)
理由如下:作AM⊥PB于M,AN⊥PE于N,
∵∠APM=∠APN
∴Rt△AMP≌Rt△ANP,
∴AM=AN,PM=PE;(5分)
∵AB=AE,
∴Rt△AMB≌Rt△ANE,
∴MB=NE∴PB+PE=(PM-MB)+(PN+NE)=2PN;(7分)
∵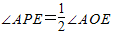 ,且ABCDE为正五边形,
,且ABCDE为正五边形,
∴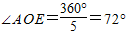 ,
,
∴∠APE=36°;
在Rt△ANP中,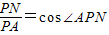 ,
,
∴PN=PA•cos36°,
∴PB+PE=2PA•cos36°.(9分)
④若P是圆内接正n边形A1A2A3…An的外接圆的 上一点时,PA2+PAn与PA1满足的数量关系是:
上一点时,PA2+PAn与PA1满足的数量关系是: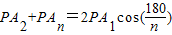 .(12分)
.(12分)
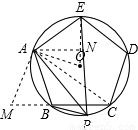
点评:正多边形的计算一般是通过中心作边的垂线,连接半径,把正多边形中的半径,边长,边心距,中心角之间的计算转化为解直角三角形.
解答:解:
③PB+PE与PA满足的数量关系是:PB+PE=2PA•cos36°;(3分)
理由如下:作AM⊥PB于M,AN⊥PE于N,
∵∠APM=∠APN
∴Rt△AMP≌Rt△ANP,
∴AM=AN,PM=PE;(5分)
∵AB=AE,
∴Rt△AMB≌Rt△ANE,
∴MB=NE∴PB+PE=(PM-MB)+(PN+NE)=2PN;(7分)
∵
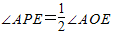 ,且ABCDE为正五边形,
,且ABCDE为正五边形,∴
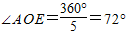 ,
,∴∠APE=36°;
在Rt△ANP中,
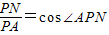 ,
,∴PN=PA•cos36°,
∴PB+PE=2PA•cos36°.(9分)
④若P是圆内接正n边形A1A2A3…An的外接圆的
 上一点时,PA2+PAn与PA1满足的数量关系是:
上一点时,PA2+PAn与PA1满足的数量关系是: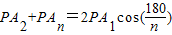 .(12分)
.(12分)
点评:正多边形的计算一般是通过中心作边的垂线,连接半径,把正多边形中的半径,边长,边心距,中心角之间的计算转化为解直角三角形.

练习册系列答案
相关题目
小颖和小红两位同学在学习“概率”时,做掷骰子(质地均匀的正方体)实验.
(1)他们在一次实验中共掷骰子60次,试验的结果如下:
①填空:此次实验中“5点朝上”的频率为 ;
②小红说:“根据实验,出现5点朝上的概率最大.”她的说法正确吗?为什么?
(2)小颖和小红在实验中如果各掷一枚骰子,那么两枚骰子朝上的点数之和为多少时的概率最大?试用列表或画树状图的方法加以说明,并求出其最大概率.
(1)他们在一次实验中共掷骰子60次,试验的结果如下:
| 朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现的次数 | 7 | 9 | 6 | 8 | 20 | 10 |
②小红说:“根据实验,出现5点朝上的概率最大.”她的说法正确吗?为什么?
(2)小颖和小红在实验中如果各掷一枚骰子,那么两枚骰子朝上的点数之和为多少时的概率最大?试用列表或画树状图的方法加以说明,并求出其最大概率.
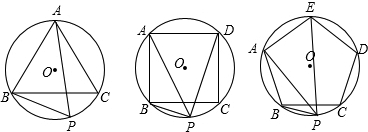


 上一点,则PB+PC=PA;
上一点,则PB+PC=PA;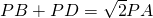 ;
;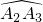 上一点,请问PA2+PAn与PA1又有怎样的数量关系,写出结论,不要求证明.
上一点,请问PA2+PAn与PA1又有怎样的数量关系,写出结论,不要求证明.