题目内容
阅读:如图①,以原点O为位似中心按比例尺(O A′:O A)3:1在位似中心的同侧将△OAB放大为△OA′B′,观察得到各点的坐标见表一,可以归纳得出:对应点的横、纵坐标均存在3倍的关系,即P(x,y)的对应点P′的坐标为(3x,3y).仿照图①,按要求完成下列画图并将坐标与归纳猜想填入表格相应.
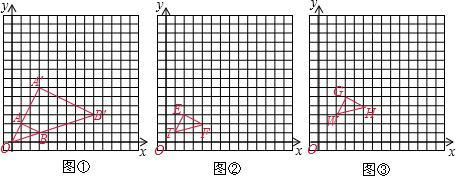
活动一:在图②中,以点T(1,1)为位似中心按比例尺(TE′:TE)3:1在位似中心的同侧将△TEF放大为△TE′F′,并将点E′、F′的坐标和归纳猜想填入表二;
活动二:在图③中,以点W(2,3)为位似中心按比例尺(WG′:WG)4:1在位似中心的同侧将△WGH放大为△WG′H′,并将点G′、H′的坐标和归纳猜想填入表三;
| 表格 | 表一 | 表二 | 表三 | |||
| 位似中心 | O(0,0) | T(1,1) | W(2,3) | |||
| 比例尺 | 3:1 | 3:1 | 4:1 | |||
| 点的坐标 | A(1,2) | B(3,1) | E(2,3) | F(4,2) | G(3,5) | H(5,4) |
| 对应点坐标 | A′(3,6) | B(9,3) | E′ | F′ | G′ | H′ |
| 猜想结论 | 点P(x,y)的对应点P′的坐标为(3x,3y) | 点P(x,y)的对应点P′的坐标为 | 点Q(x,y)的对应点Q′的坐标为 | |||
nx+a-na ny+b-nb
分析:由位似的知识可知,E′T=3ET,F′T=3FT,在图中作出点E’,点F,及点G’,点H’,可以得到各点的坐标分别为:E′(4,7),F′(10,4),G′(6,11),H′(14,7).可以得出以点M(a,b)为位似中心,按比例尺(MP′:MP)n:1在位似中心的同侧将图形放大,则点R(x,y)的对应点R′的横坐标=n(x-a)+a=nx+a-na,纵坐标=n(y-b)+a=ny+b-nb.
解答:如图:

归纳结论:以点M(a,b)为位似中心,按比例尺(MP′:MP)n:1在位似中心的同侧将图形放大,
则点R(x,y)的对应点R′的横坐标为nx+a-na,纵坐标为ny+b-nb.
点评:本题考查了位似的相关知识,位似是相似的特殊形式,位似比等于相似比.从特殊形式归纳出一般结论是应该掌握的基本数学能力.
分析:由位似的知识可知,E′T=3ET,F′T=3FT,在图中作出点E’,点F,及点G’,点H’,可以得到各点的坐标分别为:E′(4,7),F′(10,4),G′(6,11),H′(14,7).可以得出以点M(a,b)为位似中心,按比例尺(MP′:MP)n:1在位似中心的同侧将图形放大,则点R(x,y)的对应点R′的横坐标=n(x-a)+a=nx+a-na,纵坐标=n(y-b)+a=ny+b-nb.
解答:如图:

| 表格 | 表一 | 表二 | 表三 | |||
| 位似中心 | O(0,0) | T(1,1) | W(2,3) | |||
| 比例尺 | 3:1 | 3:1 | 4:1 | |||
| 点的坐标 | A(1,2) | B(3,1) | E(2,3) | F(4,2) | G(3,5) | H(5,4) |
| 对应点坐标 | A′(3,6) | B′(9,3) | E′(4,7) | F′(10,4) | G′(6,11 ) | H′( 14,7 ) |
| 猜想结论 | 点P(x,y)的对应点P′的坐标为(3x,3y) | 点P(x,y)的对应点P′的坐标为(3x-2,3y-2 ) | 点Q(x,y)的对应点Q′的坐标为(4x-6,4x-9 ) | |||
则点R(x,y)的对应点R′的横坐标为nx+a-na,纵坐标为ny+b-nb.
点评:本题考查了位似的相关知识,位似是相似的特殊形式,位似比等于相似比.从特殊形式归纳出一般结论是应该掌握的基本数学能力.

练习册系列答案
相关题目
阅读:如图①,以原点O为位似中心按比例尺(O A′:O A)3:1在位似中心的同侧将△OAB放大为△OA′B′,观察得到各点的坐标见表一,可以归纳得出:对应点的横、纵坐标均存在3倍的关系,即P(x,y)的对应点P′的坐标为(3x,3y).仿照图①,按要求完成下列画图并将坐标与归纳猜想填入表格相应.
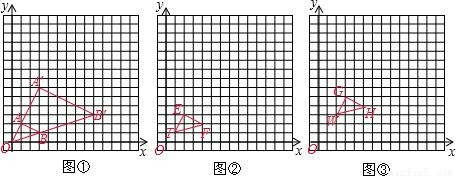
活动一:在图②中,以点T(1,1)为位似中心按比例尺(TE′:TE)3:1在位似中心的同侧将△TEF放大为△TE′F′,并将点E′、F′的坐标和归纳猜想填入表二;
活动二:在图③中,以点W(2,3)为位似中心按比例尺(WG′:WG)4:1在位似中心的同侧将△WGH放大为△WG′H′,并将点G′、H′的坐标和归纳猜想填入表三;
活动三:归纳结论:以点M(a,b)为位似中心,按比例尺(MP′:MP)n:1在位似中心的同侧将图形放大,则点R(x,y)的对应点R′的横坐标为______,纵坐标为______.

活动一:在图②中,以点T(1,1)为位似中心按比例尺(TE′:TE)3:1在位似中心的同侧将△TEF放大为△TE′F′,并将点E′、F′的坐标和归纳猜想填入表二;
活动二:在图③中,以点W(2,3)为位似中心按比例尺(WG′:WG)4:1在位似中心的同侧将△WGH放大为△WG′H′,并将点G′、H′的坐标和归纳猜想填入表三;
| 表格 | 表一 | 表二 | 表三 | |||
| 位似中心 | O(0,0) | T(1,1) | W(2,3) | |||
| 比例尺 | 3:1 | 3:1 | 4:1 | |||
| 点的坐标 | A(1,2) | B(3,1) | E(2,3) | F(4,2) | G(3,5) | H(5,4) |
| 对应点坐标 | A′(3,6) | B(9,3) | E′( ) | F′( ) | G′( ) | H′( ) |
| 猜想结论 | 点P(x,y)的对应点P′的坐标为(3x,3y) | 点P(x,y)的对应点P′的坐标为( ) | 点Q(x,y)的对应点Q′的坐标为( ) | |||
阅读:如图①,以原点O为位似中心按比例尺(O A′:O A)3:1在位似中心的同侧将△OAB放大为△OA′B′,观察得到各点的坐标见表一,可以归纳得出:对应点的横、纵坐标均存在3倍的关系,即P(x,y)的对应点P′的坐标为(3x,3y).仿照图①,按要求完成下列画图并将坐标与归纳猜想填入表格相应.
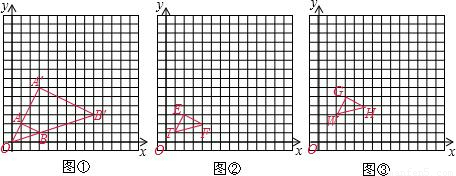
活动一:在图②中,以点T(1,1)为位似中心按比例尺(TE′:TE)3:1在位似中心的同侧将△TEF放大为△TE′F′,并将点E′、F′的坐标和归纳猜想填入表二;
活动二:在图③中,以点W(2,3)为位似中心按比例尺(WG′:WG)4:1在位似中心的同侧将△WGH放大为△WG′H′,并将点G′、H′的坐标和归纳猜想填入表三;
活动三:归纳结论:以点M(a,b)为位似中心,按比例尺(MP′:MP)n:1在位似中心的同侧将图形放大,则点R(x,y)的对应点R′的横坐标为______,纵坐标为______.

活动一:在图②中,以点T(1,1)为位似中心按比例尺(TE′:TE)3:1在位似中心的同侧将△TEF放大为△TE′F′,并将点E′、F′的坐标和归纳猜想填入表二;
活动二:在图③中,以点W(2,3)为位似中心按比例尺(WG′:WG)4:1在位似中心的同侧将△WGH放大为△WG′H′,并将点G′、H′的坐标和归纳猜想填入表三;
| 表格 | 表一 | 表二 | 表三 | |||
| 位似中心 | O(0,0) | T(1,1) | W(2,3) | |||
| 比例尺 | 3:1 | 3:1 | 4:1 | |||
| 点的坐标 | A(1,2) | B(3,1) | E(2,3) | F(4,2) | G(3,5) | H(5,4) |
| 对应点坐标 | A′(3,6) | B(9,3) | E′( ) | F′( ) | G′( ) | H′( ) |
| 猜想结论 | 点P(x,y)的对应点P′的坐标为(3x,3y) | 点P(x,y)的对应点P′的坐标为( ) | 点Q(x,y)的对应点Q′的坐标为( ) | |||
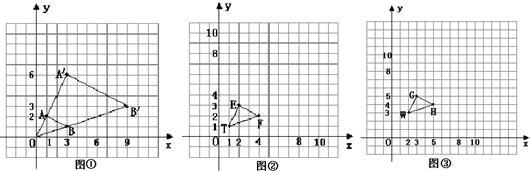

 [阅读]
[阅读]