题目内容
 [阅读]
[阅读]在平面直角坐标系中,以任意两点P(x1,y1)、Q(x2,y2)为端点的线段中点坐标为(
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
[运用]
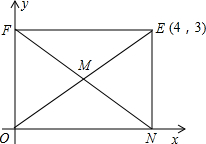
(1)如图,矩形ONEF的对角线相交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为
(2,1.5)
(2,1.5)
.(2)在直角坐标系中,有A(-1,2),B(3,1),C(1,4)、D(1,-1)四点,构成平行四边形的顶点.在该坐标系中,是否还存在一点与点A、B、C构成平行四边形的顶点?若不存在,请说明理由;若存在,请写出该点的坐标.
分析:(1)先根据四边形ONEF是矩形,所以矩形的性质可知点M是对角线OE的中点,根据题中给出的线段的中点坐标公式即可得出M点的坐标;
(2)设另一点坐标为P(x,y),再根据AP为平行四边形的对角线和BP为平行四边形的对角线两种情况进行讨论.
(2)设另一点坐标为P(x,y),再根据AP为平行四边形的对角线和BP为平行四边形的对角线两种情况进行讨论.
解答:解:(1)∵四边形ONEF是矩形,且E(4,3),
∴点M是对角线OE的中点,
∴M(
,
),即(2,1.5).
故答案为:(2,1.5);
(2)设另一点坐标为P(x,y),
当AP为平行四边形的对角线时,
∵A(-1,2),B(3,1),C(1,4),
∴
=
,
=
,解得x=5,y=3,
∴P1(5,3);
当BP为平行四边形的对角线时,
∵A(-1,2),B(3,1),C(1,4),
∴
=
,
=
,解得x=-3,y=5,
∴P2(-3,5);
当以CP为对角线时,
=
,
=
,解得x=0,y=-1,
∴P3(0,-1).
综上所述,该点的坐标为P1(5,3),P2(-3,5),P3(0,-1).
∴点M是对角线OE的中点,
∴M(
| 4 |
| 2 |
| 3 |
| 2 |
故答案为:(2,1.5);
(2)设另一点坐标为P(x,y),
当AP为平行四边形的对角线时,
∵A(-1,2),B(3,1),C(1,4),
∴
| -1+x |
| 2 |
| 3+1 |
| 2 |
| 2+y |
| 2 |
| 1+4 |
| 2 |
∴P1(5,3);
当BP为平行四边形的对角线时,
∵A(-1,2),B(3,1),C(1,4),
∴
| 3+x |
| 2 |
| -1+1 |
| 2 |
| 1+y |
| 2 |
| 2+4 |
| 2 |
∴P2(-3,5);
当以CP为对角线时,
| x+1 |
| 2 |
| -1+3 |
| 2 |
| y+4 |
| 2 |
| 2+1 |
| 2 |
∴P3(0,-1).
综上所述,该点的坐标为P1(5,3),P2(-3,5),P3(0,-1).
点评:本题考查的是四边形综合题,涉及到矩形的性质、平行四边形的性质等相关知识,难度适中.

练习册系列答案
相关题目
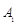 为旋转中心时,点
为旋转中心时,点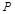 绕着点
绕着点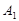 旋转180°得到
旋转180°得到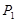 点,点
点,点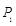 再绕着点
再绕着点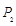 点,这时点
点,这时点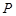 与点
与点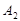 为旋转中心时,点
为旋转中心时,点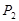 点,点
点,点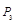 点,点
点,点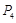 点,小明发现P、
点,小明发现P、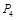 两点关于点
两点关于点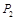 中心对称.
中心对称.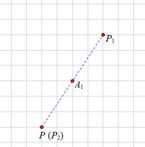
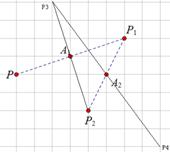
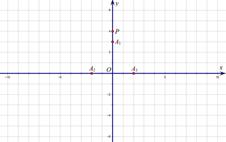
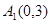 、
、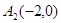 、
、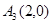 为旋转中心时,点
为旋转中心时,点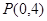 绕着点
绕着点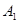 旋转180°得到
旋转180°得到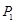 点;点
点;点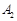 旋转180°得到
旋转180°得到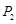 点;点
点;点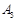 旋转180°得到
旋转180°得到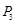 点;点
点;点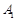 旋转180°得到点
旋转180°得到点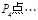 . 继续如此操作若干次得到点
. 继续如此操作若干次得到点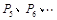 ,则点
,则点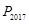 的坐为.
的坐为.