题目内容
【题目】如图，已知等边三角形OAB的顶点O(0，0)，A(0，6)，将该三角形绕点O顺时针旋转，每次旋转60°，则旋转2017次后，顶点B的坐标为_____．
【答案】
【解析】由题意知点B旋转
=6次后与点B重合，即点B的旋转周期为6，
∵2017÷6=336…1，
∴点B旋转2017次后的坐标与旋转1次后的坐标相同，
如图,OB绕点O顺时针旋转60°得到OB1,过点B1作B1C⊥x轴，
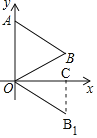
∵△OAB为等边三角形,且A(0,6)，
∴OA=OB=OB1=3,∠AOB=60°，
∴∠BOC=∠B1OC=30°，
则B1C=OB1sin∠B1OC=6×
=3,OC=OB1cos∠B1OC=6×
=
，
∴旋转2017次后,顶点B的坐标为
，
故答案为：.
练习册系列答案
相关题目
【题目】二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如表
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论：
①ac＜0；
②当x＞1时，y的值随x值的增大而减小．
③3是方程ax2+（b﹣1）x+c=0的一个根；
④当﹣1＜x＜3时，ax2+（b﹣1）x+c＞0．
其中正确的结论是 ．