题目内容
【题目】如图,在![]() 中,
中, ![]() ,点
,点![]() 为边
为边![]() 上一点,
上一点, ![]() ,且
,且![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() ,又
,又![]() 的
的![]() 边上的高为
边上的高为![]() .
.
(1)判断直线![]() 是否平行?并说明理由;
是否平行?并说明理由;
(2)证明: ![]() .
.

【答案】(1) ![]() ,理由见解析;(2)见解析
,理由见解析;(2)见解析
【解析】试题分析:(1)先根据轴对称的性质得出PC=PD,AD=AC,∠APC=∠APD,再根据三角形外角的性质求出∠APC=60°,进而求出∠BPD=60°,由条件可得BP=![]() PD,取DP的中点E,易证△BPE为等边三角形,根据等边三角形的性质和三角形外角的性质求出∠DBE=30°,进而求出∠DBP=90°,根据平行线的判定即可得出结论;
PD,取DP的中点E,易证△BPE为等边三角形,根据等边三角形的性质和三角形外角的性质求出∠DBE=30°,进而求出∠DBP=90°,根据平行线的判定即可得出结论;
(2)作ΔADP的PD边上的高为AF,又作AG⊥BD交BD的延长线于G,根据对称性得出AF=AH,再求得∠GBA=45°,证明△AGB≌△AHB,得出AG=AH=AF,根据角平分线的判定得出AD平分∠GDP,进而求得∠GDA=75°,再根据对称性求得∠CAH=∠DAF=∠GAD=15°,从而得出结论.
试题解析:
解:(1)BD//AH.
证明:∵点C关于直线PA的对称点为D,
∴PC=PD,AD=AC,∠APC=∠APD.
又∵ ∠ABC=45°,∠PAB=15°,
∴∠APC=∠ABC+∠PAB=60°,
∴∠DPB=180°-∠DPA-∠APC=60°.
∵BC=3BP,∴BP=![]() PC,
PC,
∴BP=![]() PD;
PD;
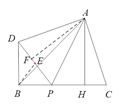
取PD的中点E,连接BE,则PE=PB,
∴△BPE为等边三角形,
∴BE=PE=DE,
∴∠DBE=∠BDE=![]() ∠BEP=30°.
∠BEP=30°.
∴∠DBP=∠DBE+∠EBP=90°.
又∵ AH⊥PC,∴∠AHC=90°,
∴∠DBP=∠AHC,∴DB//AH;
(2)证明:作ΔADP的PD边上的高为AF,又作AG⊥BD交BD的延长线于G,
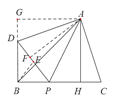
由对称性知,AF=AH.
∵∠GBA=∠GBC-∠ABC=45°,
∴∠GBA=∠HBA=45°,
∴AG=AH,
∴AG=AF,
∴AD平分∠GDP,
∴∠GDA=![]() ∠GDP=
∠GDP=![]() (180°-∠BDP) =75°.
(180°-∠BDP) =75°.
∴∠CAH=∠DAF=∠GAD=90°-∠GDA=15°,
∵∠BAP=15°,
∴∠BAP=∠CAH.