Question

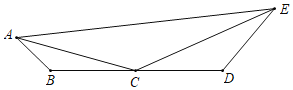
【题目】如图，在四边形ABDE中，C是BD的中点，BD＝8，AB＝2，DE＝8．若∠ACE＝150°，则线段AE长度的最大值为_____．

Answer 1

【答案】10+4．

【解析】

作B关于AC的对称点F，D关于EC的对称点G，连接AF，FC，CG，EG，FG．作CH⊥FG于H，求出AF，FG，EG，根据两点之间线段最短解决问题即可．

解：作B关于AC的对称点F，D关于EC的对称点G，连接AF，FC，CG，EG，FG．作CH⊥FG于H．

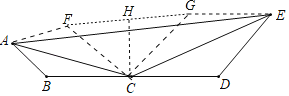
∵C是BD边的中点，

∴CB＝CD＝BD＝4

∵△ACB≌△ACF（SAS），

∴CF＝CB，∴∠BCA＝∠FCA．

同理可证：CD＝CG，∴∠DCE＝∠GCE

∵CB＝CD，∴CG＝CF

∵∠ACE＝150°，

∴∠BCA+∠DCE＝180°﹣150°＝30°．

∴∠FCA+∠GCE＝30°．

∴∠FCG＝120°．CF＝CG＝4，

∵CH⊥FG，

∴FH＝HG＝CFsin60°＝2，

∴FG＝4

∵AB＝2，DE＝8，

∴AF＝AB＝2，EG＝ED＝8

∴AE≤AF+FG+EG＝10+4．

∴当A、F、G、E共线时AE的值最大，最大值为10+4．

故答案为：10+4．