Question

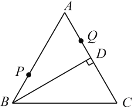
【题目】如图，是等边三角形，，点、分别为边、上的动点，当的周长最小时，的度数是______________.

Answer 1

【答案】

【解析】

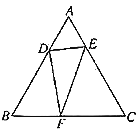
先作点D关于AC和BC的对称点G、H，连接GH交AC和BC于点E、F，此时△DEF的周长最小，再根据三角形内角和与等腰三角形的性质即可求解．

解：如图，作点D关于AC的对称点G，点D关于BC的对称点H，连接GH交AC、BC于E、F，

∵D、G关于AC对称，D、H关于BC对称，

∴DE=EG，DF=FH，

∴的周长=DE+DF+EF=EG+EF+FH,

∴当G、E、F、H四个点在同一直线上时，的周长最小，

∵是等边三角形，

∴∠A=∠B = ，

∵D、G关于AC对称，D、H关于BC对称，

∴∠ADG= ，∠BDH= ，∠EDG=∠DGE，∠FDH=∠DHF，

∴∠GDH=，

∴∠DGE+∠DHF=，

∴∠EDG+∠FDH=，

∴∠EDF=.

故答案是：.