题目内容
 (2013•黄石模拟)如图,在矩形纸片ABCD中,AB=3,BC=4.把△BCD沿对角线BD折叠,使点C落在E处,BE交AD于点F;
(2013•黄石模拟)如图,在矩形纸片ABCD中,AB=3,BC=4.把△BCD沿对角线BD折叠,使点C落在E处,BE交AD于点F;(1)求证:AF=EF;
(2)求tan∠ABF的值;
(3)连接AC交BE于点G,求AG的长.
分析:(1)由图形折叠的性质得出ED=DC,BE=BC,根据全等三角形的判定定理得出△AFB≌△EFD,由全等三角形的性质即可得出结论;
(2)设AF=x,由AB=3,BC=BE=4,AF=EF可知BF=4-x,在Rt△ABF中根据勾股定理可求出x的值,根据tan∠ABF即可得出结论;
(3)由于四边形ABCD是矩形,所以∠BAD=90°,AD∥BC,再根据勾股定理求出AC的长,由相似三角形的判定定理得出△AGF∽△CGB,所以
=
,设AG=m,则CG=5-m代入比例式即可得出m的值,进而得出结论.
(2)设AF=x,由AB=3,BC=BE=4,AF=EF可知BF=4-x,在Rt△ABF中根据勾股定理可求出x的值,根据tan∠ABF即可得出结论;
(3)由于四边形ABCD是矩形,所以∠BAD=90°,AD∥BC,再根据勾股定理求出AC的长,由相似三角形的判定定理得出△AGF∽△CGB,所以
| AF |
| BC |
| AG |
| GC |
解答:(1)证明:∵△EBD是由△CBD折叠而得,
∴ED=DC,BE=BC,
∵四边形ABCD是矩形,
∴AB=CD,∠BAD=∠BED=90°,
∴ED=AB,
∴∠ABF=∠EDF,
∵在△AFB与△EFD中,
,
∴△AFB≌△EFD(ASA),
∴AF=EF;
(2)解:设AF=x,
∵AB=3,BC=BE=4,AF=EF
∴BF=4-x,
∵∠BAF=90°
∴AF2+AB2=BF2,
∴x2+32=(4-x)2,
∴x=
,
∴tan∠ABF=
=
=
;
(3)解:∵四边形ABCD是矩形,
∴∠BAD=90°,AD∥BC;
∴AC=
=
=5,
∴△AGF∽△CGB,
∴
=
,
设AG=m,则CG=5-m,
∴
=
,
解得m=
,即AG=
.
∴ED=DC,BE=BC,
∵四边形ABCD是矩形,

∴AB=CD,∠BAD=∠BED=90°,
∴ED=AB,
∴∠ABF=∠EDF,
∵在△AFB与△EFD中,
|
∴△AFB≌△EFD(ASA),
∴AF=EF;
(2)解:设AF=x,
∵AB=3,BC=BE=4,AF=EF
∴BF=4-x,
∵∠BAF=90°
∴AF2+AB2=BF2,
∴x2+32=(4-x)2,
∴x=
| 7 |
| 8 |
∴tan∠ABF=
| AF |
| AD |
| ||
| 3 |
| 7 |
| 24 |
(3)解:∵四边形ABCD是矩形,
∴∠BAD=90°,AD∥BC;
∴AC=
| AB2+BC2 |
| 32+42 |
∴△AGF∽△CGB,
∴
| AF |
| BC |
| AG |
| GC |
设AG=m,则CG=5-m,
∴
| ||
| 4 |
| m |
| 5-m |
解得m=
| 35 |
| 39 |
| 35 |
| 39 |
点评:本题考查的是相似三角形的判定与性质,涉及到全等三角形的判定与性质、矩形的性质及勾股定理,熟知以上知识是解答此题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
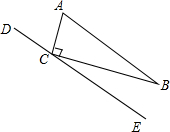 (2013•黄石模拟)如图,Rt△ABC中,∠ACB=90°,DE经过点C且平行于AB,∠A=65°,则∠BCE的度数是( )
(2013•黄石模拟)如图,Rt△ABC中,∠ACB=90°,DE经过点C且平行于AB,∠A=65°,则∠BCE的度数是( )