题目内容
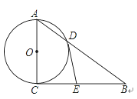
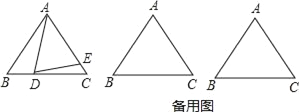
【题目】如图,已知△ABC中,AB=AC=6,BC=8,点D是BC边上的一个动点,点E在AC边上,∠ADE=∠B.设BD的长为x,CE的长为y.
(1)当D为BC的中点时,求CE的长;
(2)求y关于x的函数关系式,并写出x的取值范围;
(3)如果△ADE为等腰三角形,求x的值.
【答案】(1)![]() ;(2) y=﹣
;(2) y=﹣![]() x2+
x2+![]() x(0≤x<8);(3) 2或
x(0≤x<8);(3) 2或![]() .
.
【解析】
(1)先根据等腰三角形的性质由AB=AC得∠B=∠C,再利用三角形外角性质得∠ADC=∠ADE+∠CDE=∠B+∠BAD,加上∠ADE=∠B,则∠BAD=∠CDE,根据相似三角形的判定方法待定△ABD∽△DCE,利用相似比得到y=-![]() x2+
x2+![]() x(0≤x≤8),然后把x=4代入计算得到CE的长为
x(0≤x≤8),然后把x=4代入计算得到CE的长为![]() ;
;
(2)由(1)得到y关于x的函数关系式为y=-![]() x2+
x2+![]() x(0≤x≤8);
x(0≤x≤8);
(3)由于∠AED>∠C,而∠B=∠ADE=∠C,则∠AED>∠ADE,所以AE<AD,然后分类讨论:当DA=DE时,利用△ABD∽△DCE得到![]() =1,即x=y,得到一元二次方程-
=1,即x=y,得到一元二次方程-![]() x2+
x2+![]() x=x,解方程得x1=0(舍去),x2=2;当EA=ED时,得到∠EAD=∠ADE,而∠ADE=∠C,所以∠EAD=∠C,可判断△DAC∽△ABC,利用相似比得到
x=x,解方程得x1=0(舍去),x2=2;当EA=ED时,得到∠EAD=∠ADE,而∠ADE=∠C,所以∠EAD=∠C,可判断△DAC∽△ABC,利用相似比得到![]() =
=![]() ,解得x=
,解得x=![]() .
.
解:(1)∵AB=AC,
∴∠B=∠C,
∵∠ADC=∠ADE+∠CDE=∠B+∠BAD,
而∠ADE=∠B,
∴∠BAD=∠CDE,
∴△ABD∽△DCE,
∴![]() ,
,
∴y=-![]() x2+
x2+![]() x,
x,
当x=4时, y=-![]() ×16+
×16+![]() ×4=
×4=![]() ,
,
即当D为BC的中点时,CE的长为![]() ;
;
(2)由(1)得y关于x的函数关系式为y=-![]() x2+
x2+![]() x(0≤x≤8);
x(0≤x≤8);
(3)∵∠AED>∠C,
而∠B=∠ADE=∠C,
∴∠AED>∠ADE,
∴AE<AD,
当DA=DE时,
∵△ABD∽△DCE,
∴![]() ,即
,即![]() =1,
=1,
∴x=y,
∴-![]() x2+
x2+![]() x=x,解得x1=0(舍去),x2=2,
x=x,解得x1=0(舍去),x2=2,
当EA=ED时,则∠EAD=∠ADE,
而∠ADE=∠C,
∴∠EAD=∠C,
∴△DAC∽△ABC,
∴![]() ,即
,即![]() =
=![]() ,
,
∴x=![]() ,
,
综上所述,当△ADE为等腰三角形,x的值为2或![]() .
.