Question

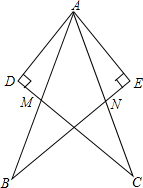
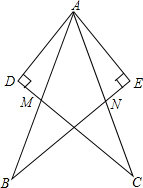
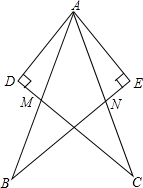
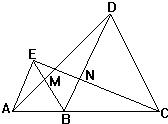
如图: 在△AEB和△ADC中,给出以下四个论断：(1)AB=AC;(2)AD=AE;

(3)AM=AN;(4)AD⊥DC,AE⊥BE.以其中三个论断为题设,填入下面的“已知”栏中,一个论断为结论,填入下面的“求证”栏中，使之组成一个真命题，并写出证明过程。

如图，在△AEB和△ADC中，已知：＿＿＿＿＿＿＿＿＿＿＿＿＿＿.（3分）

   求证: ＿＿＿＿＿＿＿.（1分）

   证明:（8分）                               

                                                                                                     

 

Answer 1

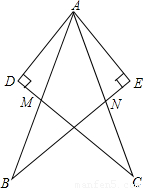
【答案】

① ② ④ （3分） AM=AN（4分）

在△AEB和△ADC中，

∵ AB=AC

 AD=AE                      △AEB≌△ADC （7分）

   AD⊥DC，AE⊥BE

∴∠EAN=∠DAM （8分）  因此可得：△AEN≌△ADM （11分）

∴AM=AN （12分）

【解析】先确定选择哪对三角形，再对应三角形全等条件证明全等．利用全等三角形对应角，对应边相等解题．