题目内容
【题目】在正方形![]() 中,
中,![]() 是
是![]() 边上一点,
边上一点,
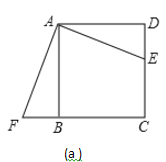
(1)将![]() 绕点
绕点![]() 按顺时针方向旋转。使
按顺时针方向旋转。使![]() 、
、![]() 重合,得到
重合,得到![]() ,如图(a)所示.观察可知:与
,如图(a)所示.观察可知:与![]() 相等的线段是__________,
相等的线段是__________,![]() __________.
__________.
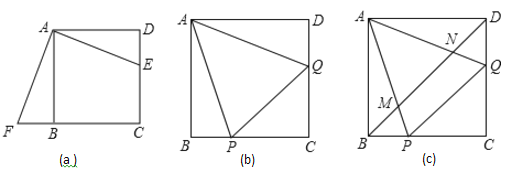
(2)如图(b)所示,正方形![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 边上的点,且
边上的点,且![]() ,试通过旋转的方式说明:
,试通过旋转的方式说明:![]() .
.
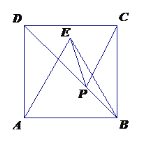
(3)在(2)的条件下,连接![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,如图(c)所示.判断
,如图(c)所示.判断![]() 、
、![]() 、
、![]() 之间的关系,直接写出结论.
之间的关系,直接写出结论.
【答案】(1)![]() ,
,![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)如图(a),直接根据旋转的性质得到DE=BF,∠AFB=∠AED;
(2)将△ADQ绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABE,根据旋转的性质得∠EAQ=∠BAD=90°,AE=AQ,BE=DQ,而∠PAQ=45°,则∠PAE=45°,再根据全等三角形的判定方法得到△APE≌△APQ,则PE=PQ,于是PE=PB+BE=PB+DQ,即可得到DQ+BP=PQ;
(3)根据正方形的性质有∠ABD=∠ADB=45°,将△ADN绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABK,根据旋转的性质得∠ABK=∠ADN=45°,BK=DN,AK=AN,与(2)一样可证明△AMN≌△AMK得到MN=MK,由于∠MBK=∠MBA+∠KBA=45°+45°=90°,得到△BMK为直角三角形,根据勾股定理得BK2+BM2=MK2,然后利用等相等代换即可得到BM2+DN2=MN2.
(1)如图(a).
∵△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF.
∵DE=BF,∠AFB=∠AED.
故答案为:BF,AED;
(2)将△ADQ绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABE,如图2,
则∠D=∠ABE=90°,即点E、B、P共线,∠EAQ=∠BAD=90°,AE=AQ,BE=DQ.
∵∠PAQ=45°,
∴∠PAE=45°,
∴∠PAQ=∠PAE,
在△APE和△APQ中,
∵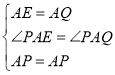 ,
,
∴△APE≌△APQ(SAS),
∴PE=PQ,
而PE=PB+BE=PB+DQ,
∴DQ+BP=PQ;
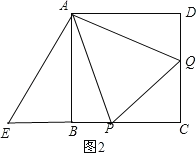
(3)BM2+DN2=MN2.证明如下:
∵四边形ABCD为正方形,
∴∠ABD=∠ADB=45°,
如图3,将△ADN绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABK,
则∠ABK=∠ADN=45°,BK=DN,AK=AN,
与(2)一样可证明△AMN≌△AMK,得到MN=MK.
∵∠MBK=∠MBA+∠KBA=45°+45°=90°,
∴△BMK为直角三角形,
∴BK2+BM2=MK2,
∴BM2+DN2=MN2.

 名校课堂系列答案
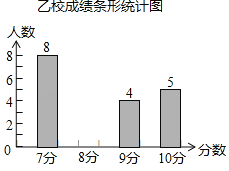
名校课堂系列答案【题目】甲、乙两校参加学生英语口语比赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分),乙校平均分是8.3分,乙校的中位数是8分.依据统计数据绘制了如下尚不完整的甲校成绩统计表和乙校成绩统计图;
甲校成绩统计表
分数 | 7分 | 8分 | 9分 | 10分 |
人数 | 11 | 0 | ■ | 8 |
(1)请你将乙校成绩统计图直接补充完整;
(2)请直接写出甲校的平均分是 ,甲校的中位数是 ,甲校的众数是 ,从平均分和中位数的角度分析 校成绩较好(填“甲”或“乙”).