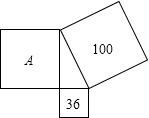
题目内容
在△ABC中，若∠ACB=120°，AC=BC，AB边上的高CD=3，则AC=______，AB=______，BC边上的高AE=______．
∵在△ABC中，若∠ACB=120°，AC=BC，
∴∠CAB=∠CBA=30°．
又∵CD⊥AB，
∴AC=2CD=6（30°角所对的直角边是斜边的一半），AD=BD．
在Rt△ACD中，AD=
=
=3
．
则AB=2AD=6
．
∵S△ABC=
AB•CD=
BC•AE，
∴AE=
=3
．
故答案分别是：6；6
；3
．
∴∠CAB=∠CBA=30°．
又∵CD⊥AB，
∴AC=2CD=6（30°角所对的直角边是斜边的一半），AD=BD．
在Rt△ACD中，AD=
| AC2-CD2 |
| 62-32 |
| 3 |
则AB=2AD=6
| 3 |
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴AE=
6
| ||
| 6 |
| 3 |
故答案分别是：6；6
| 3 |
| 3 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
