题目内容
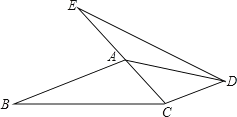
【题目】已知:如图,点E、A、C在同一条直线上,AB∥CD,AB=CE,∠B=∠E.
(1)求证:△ABC≌△CED;
(2)若∠B=25°,∠ACB=45°,求∠ADE的度数.
【答案】(1)证明见解析,(2)10°.
【解析】试题分析:(1)根据平行线得出∠BAC=∠ECD,结合题目中的已知条件得出三角形全等;(2)根据三角形全等得出CA=CD,即∠CAD=∠CDA,然后根据三角形外角的性质以及角度之间的关系求出答案.
试题解析:(1)∵AB∥CD,∴∠BAC=∠ECD,又∵∠B=∠E,AB=CE,
∴△ABC≌△CED;
(2)∵△ABC≌△CED, ∴∠E=∠B=25°,∠EDC=∠ACB=45°,CA=CD,
∴∠CAD=∠CDA, 设∠ADE=x, 根据外角的性质可知:∠CAD=∠E+∠ADE=25°+x,
∴25°+x=45°-x,解得:x=10°,即∠ADE=10°.

练习册系列答案
相关题目