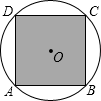
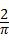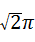题目内容
 若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是
若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是
- A.

- B.
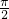
- C.
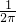
- D.
 π
π
A
分析:在这个圆面上随意抛一粒豆子,落在圆内每一个地方是均等的,因此计算出正方形和圆的面积,利用几何概率的计算方法解答即可.
解答:设⊙O的直径为2a,则半径为a,⊙O的面积为πa2;
正方形的边长为:AD=CD= ×2a=
×2a= a,面积为2a2;
a,面积为2a2;
因为豆子落在圆内每一个地方是均等的,
所以P(豆子落在正方形ABCD内)= =
=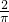 .
.
故选:A.
点评:此题主要考查了正多边形和圆以及几何概率的意义:一般地,对于古典概型,如果试验的基本事件为n,随机事件A所包含的基本事件数为m,我们就用来描述事件A出现的可能性大小,称它为事件A的概率,记作P(A),即有 P(A)=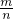 .
.
分析:在这个圆面上随意抛一粒豆子,落在圆内每一个地方是均等的,因此计算出正方形和圆的面积,利用几何概率的计算方法解答即可.
解答:设⊙O的直径为2a,则半径为a,⊙O的面积为πa2;
正方形的边长为:AD=CD=
 ×2a=
×2a= a,面积为2a2;
a,面积为2a2;因为豆子落在圆内每一个地方是均等的,
所以P(豆子落在正方形ABCD内)=
 =
=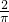 .
.故选:A.
点评:此题主要考查了正多边形和圆以及几何概率的意义:一般地,对于古典概型,如果试验的基本事件为n,随机事件A所包含的基本事件数为m,我们就用来描述事件A出现的可能性大小,称它为事件A的概率,记作P(A),即有 P(A)=
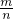 .
. 
练习册系列答案
相关题目
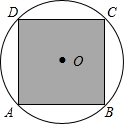 如图,正方形ABCD内接于⊙O,⊙O的直径为
如图,正方形ABCD内接于⊙O,⊙O的直径为| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( )
若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( ) 如图,正方形ABCD内接于⊙O,⊙O的直径为
如图,正方形ABCD内接于⊙O,⊙O的直径为 分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( )
分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( )