题目内容
(2002•大连)观察下列数表1 2 3 4 …第一行
2 3 4 5 …第二行
3 4 5 6 …第三行
4 5 6 7 …第四行
…
第第第第
一二三四
列列列列
根据数表反映的规律,猜想第6行与第6列的交叉点上的数应为 ,第n行与第n列的交叉点上的数应为 (用含正整数n的式子表示).
【答案】分析:根据题意,观察可得规律为第n行第一个数为n,且后一个比前一个大1,进而可得第6行与第6列的交叉点上的数与第n行与第n列的交叉点上的数.
解答:解:根据题意,观察可得:
第一行第一个数为1,后一个比前一个大1;
第二行第一个数为2,后一个比前一个大1;
…
第6行第一个数为2,后一个比前一个大1,则第6列的数为6+6-1=11;
其规律为第n行第一个数为n,且后一个比前一个大1;
则第n行与第n列的交叉点上的数,即第n行的第n个数为n+n-1=2n-1;
故答案为11,2n-1.
点评:处理此类问题,要仔细观察、认真分析,发现规律,最后要注意验证所找出的规律.
解答:解:根据题意,观察可得:
第一行第一个数为1,后一个比前一个大1;
第二行第一个数为2,后一个比前一个大1;
…
第6行第一个数为2,后一个比前一个大1,则第6列的数为6+6-1=11;
其规律为第n行第一个数为n,且后一个比前一个大1;
则第n行与第n列的交叉点上的数,即第n行的第n个数为n+n-1=2n-1;
故答案为11,2n-1.
点评:处理此类问题,要仔细观察、认真分析,发现规律,最后要注意验证所找出的规律.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
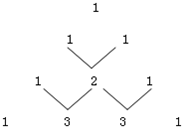 28、如图是杨辉三角系数表,它的作用是指导读者按规律写出行如(a+b)n展开式的系数,请你仔细观察下表中的规律,填出展开式中所缺的系数.
28、如图是杨辉三角系数表,它的作用是指导读者按规律写出行如(a+b)n展开式的系数,请你仔细观察下表中的规律,填出展开式中所缺的系数. ”的个数是“
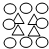
”的个数是“ ”的5倍( )
”的5倍( )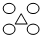

 如图是杨辉三角系数表,它的作用是指导读者按规律写出行如(a+b)n展开式的系数,请你仔细观察下表中的规律,填出展开式中所缺的系数.
如图是杨辉三角系数表,它的作用是指导读者按规律写出行如(a+b)n展开式的系数,请你仔细观察下表中的规律,填出展开式中所缺的系数.