题目内容
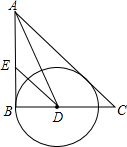 (2013•响水县一模)如图,在△ABC中,∠B=90°,∠A的平分线交BC于D,以D为圆心,DB长为半径作⊙D
(2013•响水县一模)如图,在△ABC中,∠B=90°,∠A的平分线交BC于D,以D为圆心,DB长为半径作⊙D(1)试判断直线AC与⊙D的位置关系,并说明理由;
(2)若点E在AB上,且DE=DC,当AB=3,AC=5时,求线段AE长.
分析:(1)过点D作DF⊥AC于F,求出BD=DF等于半径,得出AC是⊙D的切线.
(2)首先证明Rt△ABD≌Rt△AFD可得AB=AF=3,进而得到FC=2,再证明Rt△EBD≌Rt△CFD进而得到EB=FC,继而得到AE=1.
(2)首先证明Rt△ABD≌Rt△AFD可得AB=AF=3,进而得到FC=2,再证明Rt△EBD≌Rt△CFD进而得到EB=FC,继而得到AE=1.
解答: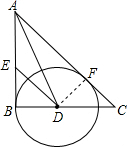 解:(1)AC与⊙D相切;
解:(1)AC与⊙D相切;
理由如下:
过点D作DF⊥AC于F;
∵AB为⊙D的切线,AD平分∠BAC,
∴BD=DF,
∴AC为⊙D的切线;
(2)∵在Rt△ABD和Rt△AFD中
,
∴Rt△ABD≌Rt△AFD(HL),
∴AB=AF=3,
∵AC=5,
∴FC=2,
∵在Rt△EBD和Rt△CFD中
,
∴Rt△EBD≌Rt△CFD(HL),
∴EB=FC=2,
∴AE=3-2=1.
 解:(1)AC与⊙D相切;
解:(1)AC与⊙D相切;理由如下:
过点D作DF⊥AC于F;
∵AB为⊙D的切线,AD平分∠BAC,
∴BD=DF,
∴AC为⊙D的切线;
(2)∵在Rt△ABD和Rt△AFD中
|
∴Rt△ABD≌Rt△AFD(HL),
∴AB=AF=3,
∵AC=5,
∴FC=2,
∵在Rt△EBD和Rt△CFD中
|
∴Rt△EBD≌Rt△CFD(HL),
∴EB=FC=2,
∴AE=3-2=1.
点评:此题主要考查了全等三角形的判定与性质,以及切线的判定,关键是掌握全等三角形的判定与性质定理.

练习册系列答案
相关题目
 (2013•响水县一模)兴趣小组的同学要测量教学楼前一棵树的高度.在阳光下,一名同学测得一根竖直在地面上的长为1米的竹竿的在地面上的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此台阶上影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,则此树高为多少米?
(2013•响水县一模)兴趣小组的同学要测量教学楼前一棵树的高度.在阳光下,一名同学测得一根竖直在地面上的长为1米的竹竿的在地面上的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此台阶上影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,则此树高为多少米? (2013•响水县一模)如图,正方形ABCD和EFGC中,正方形EFGC的边长为a,用a的代数式表示阴影部分△AEG的面积为( )
(2013•响水县一模)如图,正方形ABCD和EFGC中,正方形EFGC的边长为a,用a的代数式表示阴影部分△AEG的面积为( )