题目内容
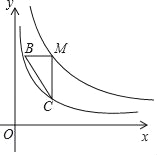
【题目】如图,点M在函数y=![]() (x>0)的图象上,过点M分别作x轴和y轴的平行线交函数y=
(x>0)的图象上,过点M分别作x轴和y轴的平行线交函数y=![]() (x>0)的图象于点B、C.
(x>0)的图象于点B、C.
(1)若点M的坐标为(1,3).
①求B、C两点的坐标;
②求直线BC的解析式;
(2)求△BMC的面积.
【答案】(1)①B(![]() ,3),C(1,1);②y=﹣3x+4;(2)
,3),C(1,1);②y=﹣3x+4;(2)![]()
【解析】(1)把点M横纵坐标分别代入![]() 解析式得到点B、C坐标,应用待定系数法求BC解析式;
解析式得到点B、C坐标,应用待定系数法求BC解析式;
(2)设出点M坐标(a,b),利用反比例函数性质,ab=3,用a、b表示BM、MC,求△BMC的面积.
(1)①∵点M的坐标为(1,3)
且B、C函数![]() (x>0)的图象上
(x>0)的图象上
∴点C横坐标为1,纵坐标为1,
点B纵坐标为3,横坐标为![]()
∴点C坐标为(1,1),点B坐标为![]()
②设直线BC解析式为![]()
把B、C点坐标代入得
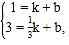
解得
![]()
∴直线BC解析式为:![]()
(2)设点M坐标为(a,b),
∵点M在函数![]() (x>0)的图象上
(x>0)的图象上
∴ab=3
由(1)点C坐标为![]() B点坐标为
B点坐标为![]()
∴![]()
∴![]()

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
【题目】某村在推进美丽乡村活动中,决定建设幸福广场,计划铺设相同大小规格的红色和蓝色地砖.经过调査.获取信息如下:
购买数量低于5000块 | 购买数量不低于5000块 | |
红色地砖 | 原价销售 | 以八折销售 |
蓝色地砖 | 原价销售 | 以九折销售 |
如果购买红色地砖4000块,蓝色地砖6000块,需付款86000元;如果购买红色地砖10000块,蓝色地砖3500块,需付款99000元.
(1)红色地砖与蓝色地砖的单价各多少元?
(2)经过测算,需要购置地砖12000块,其中蓝色地砖的数量不少于红色地砖的一半,并且不超过6000块,如何购买付款最少?请说明理由.