题目内容
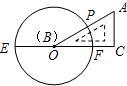20、如图，已知EF是⊙O的直径，把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上，斜边AB与⊙O交于点P，点B与点O重合；将三角形ABC沿OE方向平移，使得点B与点E重合为止．设∠POF=x°，则x的取值范围是30≤x≤60
．分析：在移动的过程中，x的最小值即点B和点O重合时，即是90°-60°=30°．
x的最大值即当点B和点E重合时，根据圆周角定理，得x=30°×2=60°．
由此可求出x的取值范围．
x的最大值即当点B和点E重合时，根据圆周角定理，得x=30°×2=60°．
由此可求出x的取值范围．
解答：解：当O、B重合时，∠POF的度数最小，∠POF=x=30°；
当B、E重合时，∠POF的度数最大，∠POF=x=2∠ABC=60°；
故x的取值范围是30°≤x≤60°．
当B、E重合时，∠POF的度数最大，∠POF=x=2∠ABC=60°；
故x的取值范围是30°≤x≤60°．
点评：解决本题的关键是能够分析出x取最大值和最小值时B点的位置．
练习册系列答案
阅读快车系列答案
相关题目
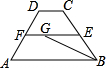如图，已知EF是梯形ABCD的中位线，若AB=8，BC=6，CD=2，∠B的平分线交EF于G，则FG的长是
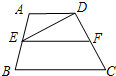如图，已知EF是梯形ABCD的中位线，△DEF的面积为4cm2，则梯形ABCD的面积为
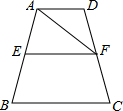（2013•当涂县模拟）如图，已知EF是梯形ABCD的中位线，连接AF，若△AEF的面积为6cm2，则梯形ABCD的面积为
在证明三角形中位线性质“如图，已知EF是△ABC的中位线，求证：EF∥BC，EF=