题目内容
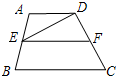 如图,已知EF是梯形ABCD的中位线,△DEF的面积为4cm2,则梯形ABCD的面积为
如图,已知EF是梯形ABCD的中位线,△DEF的面积为4cm2,则梯形ABCD的面积为分析:设梯形的高为h,根据已知△DEF的高为梯形高的一半,从而根据三角形的面积可求得中位线与高的乘积,即求得了梯形的面积.
解答:解:设梯形的高为h,
∵EF是梯形ABCD的中位线,
∴△DEF的高为
,
∵△DEF的面积为
×EF×
=
h•EF=4,
∴h•EF=16,
∴梯形ABCD的面积为EF•h=16.
∵EF是梯形ABCD的中位线,
∴△DEF的高为
| h |
| 2 |
∵△DEF的面积为
| 1 |
| 2 |
| h |
| 2 |
| 1 |
| 4 |
∴h•EF=16,
∴梯形ABCD的面积为EF•h=16.
点评:此题主要考查梯形中位线定理的运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
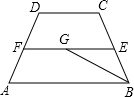 如图,已知EF是梯形ABCD的中位线,若AB=8,BC=6,CD=2,∠B的平分线交EF于G,则FG的长是( )
如图,已知EF是梯形ABCD的中位线,若AB=8,BC=6,CD=2,∠B的平分线交EF于G,则FG的长是( )| A、1 | B、1.5 | C、2 | D、2.5 |
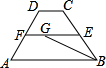 如图,已知EF是梯形ABCD的中位线,若AB=8,BC=6,CD=2,∠B的平分线交EF于G,则FG的长是
如图,已知EF是梯形ABCD的中位线,若AB=8,BC=6,CD=2,∠B的平分线交EF于G,则FG的长是 如图,已知EF是梯形ABCD的中位线,若梯形ABCD的面积为16cm2,则△DEF的面积为
如图,已知EF是梯形ABCD的中位线,若梯形ABCD的面积为16cm2,则△DEF的面积为 (2013•当涂县模拟)如图,已知EF是梯形ABCD的中位线,连接AF,若△AEF的面积为6cm2,则梯形ABCD的面积为
(2013•当涂县模拟)如图,已知EF是梯形ABCD的中位线,连接AF,若△AEF的面积为6cm2,则梯形ABCD的面积为