题目内容
(本题8分)如图,四边形 中,
中,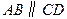 ,
, 平分
平分 ,
, 交
交 于
于 .
.
(1)求证:四边形
 是菱形;
是菱形;(2)若点
 是
是 的中点,试判断
的中点,试判断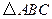 的形状,并说明理由.
的形状,并说明理由.
证明:
(1)∵AB∥CD,即AE∥CD,
又∵CE∥AD,∴四边形AECD是平行四边形. 2分
∵AC平分∠BAD,∴∠CAE=∠CAD,
又∵AD∥CE,∴∠ACE=∠CAD,
∴∠ACE=∠CAE,
∴AE=CE,
∴四边形AECD是菱形;········· 4分
(2)证法一:∵E是AB中点,∴AE=BE.
又∵AE=CE,∴BE=CE,∴∠B=∠BCE,
∵∠B+∠BCA+∠BAC=180°,
∴2∠BCE+2∠ACE=180°,∴∠BCE+∠ACE=90°.
即∠ACB=90°,∴△ABC是直角三角形.
证法二:连DE,则DE⊥AC,且平分AC,
设DE交AC于F,∵E是AB的中点,∴EF∥BC.
∴BC⊥AC,∴△ABC是直角三角形.······· 8分解析:
略
(1)∵AB∥CD,即AE∥CD,
又∵CE∥AD,∴四边形AECD是平行四边形. 2分
∵AC平分∠BAD,∴∠CAE=∠CAD,
又∵AD∥CE,∴∠ACE=∠CAD,
∴∠ACE=∠CAE,
∴AE=CE,
∴四边形AECD是菱形;········· 4分
(2)证法一:∵E是AB中点,∴AE=BE.
又∵AE=CE,∴BE=CE,∴∠B=∠BCE,
∵∠B+∠BCA+∠BAC=180°,
∴2∠BCE+2∠ACE=180°,∴∠BCE+∠ACE=90°.
即∠ACB=90°,∴△ABC是直角三角形.
证法二:连DE,则DE⊥AC,且平分AC,
设DE交AC于F,∵E是AB的中点,∴EF∥BC.
∴BC⊥AC,∴△ABC是直角三角形.······· 8分解析:
略

练习册系列答案
相关题目





 于D.
于D.
 于D.
于D.