题目内容
（原创题）如图所示，扇形OAB从图①无滑动旋转到图②，再由图②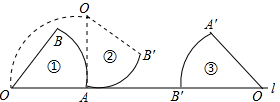
到图③，∠O=60°，OA=1．（1）求O点所运动的路径长；
（2）O点走过路径与直线L围成的面积．
分析：本题一共转动了三次，关键是分析每一次转动的圆心角和半径，然后利用弧长公式求．
解答：解：（1）运动路径第一段弧长
=
，
第二段路径为线段长为
=
，
第三段路径为
=
，
即O在L上运动路径为
+
+
=
．
（2）围成面积，
S1=
=
π，S2=1×
=
，S3=
=
，S=S1+S2+S3=
．
| 90π×1 |
| 180 |
| π |
| 2 |
第二段路径为线段长为
| 60π • 1 |
| 180 |
| π |
| 3 |
第三段路径为
| 90π • 1 |
| 180 |
| π |
| 2 |
即O在L上运动路径为
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 4π |
| 3 |
（2）围成面积，
S1=
| 90π • 1 |
| 360 |
| 1 |
| 4 |
| π |
| 3 |
| π |
| 3 |
| 90π • 1 |
| 360 |
| π |
| 4 |
| 5π |
| 6 |
点评：本题的难点是第二次，实际上就是扇形的弧长，其它二次则简单．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
58、（原创题）如图所示，在∠AOB内有一点P．
61、（原创题）如图所示，在书写艺术字时，常常运用画“平行线段”这种基本作图方法，此图是在书写字母“M”：
（原创题）如图所示，平面直角坐标系中，点A（2，9），B（2，3），C（3，2），D（9，2）在⊙P上，Q是⊙P上的一个动点．
30、（原创题）如图所示，L1∥L2，CD⊥L2垂足为C，AO与L1交于B，与CD交于点O，若∠AOD=130°，求∠1的度数．