题目内容
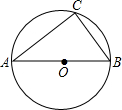 (2012•宜昌二模)如图,⊙O的直径AB=5,弦BC=3,tanB=( )
(2012•宜昌二模)如图,⊙O的直径AB=5,弦BC=3,tanB=( )分析:由AB是⊙O的直径,根据直径所对的圆周角是直角,可得∠C=90°,然后由勾股定理求得AC的长,再由余弦函数的定义求得答案.
解答:解:∵AB是⊙O的直径,
∴∠C=90°,
∵AB=5,BC=3,
∴AC=
=4,
∴tanB=
=
.
故选D.
∴∠C=90°,
∵AB=5,BC=3,
∴AC=
| AB2-BC2 |
∴tanB=
| AC |
| BC |
| 4 |
| 3 |
故选D.
点评:此题考查了圆周角定理、勾股定理以及余弦函数的定义.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
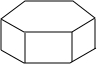 (2012•宜昌二模)如图是一个底面为正六边形的棱柱,这个棱柱的左视图是( )
(2012•宜昌二模)如图是一个底面为正六边形的棱柱,这个棱柱的左视图是( )