题目内容
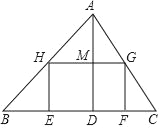
【题目】如图,△ABC的面积为12,BC与BC边上的高AD之比为3:2,矩形EFGH的边EF在BC上,点H,G分别在边AB、AC上,且HG=2GF.
(1)求AD的长;
(2)求矩形EFGH的面积.
【答案】(1)AD=4;(2)矩形EFGH的面积![]() .
.
【解析】
(1)设BC=3x,根据三角形的面积公式列式计算即可;
(2)设GF=y,根据矩形的性质得到HG∥BC,得到△AHG∽△ABC,根据相似三角形的性质列出比例式,计算即可.
(1)设BC=3x,则AD=2x,
∵△ABC的面积为12,
∴![]() ×3x×2x=12,
×3x×2x=12,
解得,x1=2,x2=﹣2(舍去),
则AD的长=2x=4;
(2)设GF=y,则HG=2y,
∵四边形EFGH为矩形,
∴HG∥BC,
∴△AHG∽△ABC,
∴![]() ,即
,即![]() ,
,
解得,y=![]() ,
,
HG=2y=![]() ,
,
则矩形EFGH的面积=![]() ×
×![]() =
=![]() .
.

练习册系列答案
相关题目
【题目】已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
| ﹣4 |
| ﹣4 |
| 0 |
| … |
(1)求该抛物线的表达式;
(2)已知点E(4, y)是该抛物线上的点,点E关于抛物线的对称轴对称的点为点F,求点E和点F的坐标.