题目内容
【题目】如图，△ABC是等边三角形，△ADE是等腰三角形，AD=AE，∠DAE=80°，当DE⊥AC时，垂足为F，求∠BAD和∠EDC的度数．
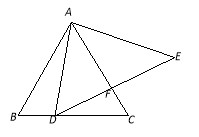
【答案】∠BAD=20°；∠EDC=30°
【解析】
试题分析：根据DE⊥AC，AD=AE，∠DAE=80°得出∠ADE=∠E=50°，∠DAF=∠EAF=40°，根据等边三角形的性质得出∠BAD的度数，根据三角形内角和定理得出∠EDC的度数.
试题解析：当DE⊥AC时， ∵AD=AE，∠DAE=80° ∴∠ADE=∠E=50° ∠DAF=∠EAF=40°
∵△ABC是等边三角形 ∴∠BAC=60° ∴∠BAD=60°﹣40°=20°
∵∠B+∠BAD=∠ADE+∠EDC ∴60°+20°=50°+∠EDC ∴∠EDC=30°
练习册系列答案
相关题目
