题目内容
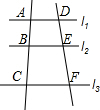
 如图,已知l1∥l2∥l3,矩形ABCD的四个顶点在l1、l2、l3上,过B作EF⊥l2,分别交l1、l3于E、F,若AE=1,FC=4,则l1与l2之间的距离是
如图,已知l1∥l2∥l3,矩形ABCD的四个顶点在l1、l2、l3上,过B作EF⊥l2,分别交l1、l3于E、F,若AE=1,FC=4,则l1与l2之间的距离是2
2
.分析:过点C作CG⊥BD于点G,根据两直线平行,内错角相等可得∠1=∠2=∠3,然后利用“角角边”证明△ABE和△DCG全等,根据全等三角形对应边相等可得CG=BE,再根据平行线间的距离相等可得CG=BF,所以,BE=BF,然后判定出△ABE和△BCF相似,根据相似三角形对应边成比例列出比例式求解即可.
解答: 解:如图,过点C作CG⊥BD于点G,
解:如图,过点C作CG⊥BD于点G,
∵l1∥l2,
∴∠1=∠2,
∴矩形的边AB∥CD,
∴∠2=∠3,
∴∠1=∠2=∠3,
在△ABE和△DCG中,
,
∴△ABE≌△DCG(AAS),
∴CG=BE,
根据平行线间的距离相等可得CG=BF,
∴BE=BF,
∵∠1+∠4=90°,
∠4+∠5=180°-90°=90°,
∴∠1=∠5,
又∵∠AEB=∠BFC=90°,
∴△ABE∽△BCF,
∴
=
,
∵AE=1,FC=4,BE=BF,
∴
=
,
解得BE=2.
故答案为:2.
 解:如图,过点C作CG⊥BD于点G,
解:如图,过点C作CG⊥BD于点G,∵l1∥l2,
∴∠1=∠2,
∴矩形的边AB∥CD,
∴∠2=∠3,
∴∠1=∠2=∠3,
在△ABE和△DCG中,
|
∴△ABE≌△DCG(AAS),
∴CG=BE,
根据平行线间的距离相等可得CG=BF,
∴BE=BF,
∵∠1+∠4=90°,
∠4+∠5=180°-90°=90°,
∴∠1=∠5,
又∵∠AEB=∠BFC=90°,
∴△ABE∽△BCF,
∴
| AE |
| BF |
| BE |
| FC |
∵AE=1,FC=4,BE=BF,
∴
| 1 |
| BE |
| BE |
| 4 |
解得BE=2.
故答案为:2.
点评:本题考查了相似三角形的判定与性质,全等三角形的判定与性质,矩形的对边平行且相等的性质,作辅助线,利用全等三角形证明得到l2与l3之间的距离等于l1与l2之间的距离是解题的关键.

练习册系列答案
相关题目
 如图,已知l1∥l2∥l3,若AB:BC=3:5,DF=16,则DE=
如图,已知l1∥l2∥l3,若AB:BC=3:5,DF=16,则DE= (2012•甘孜州)如图,已知l1∥l2∥l3∥l4,相邻两条平行线间的距离都相等,如果正方形ABCD的四个顶点分别在四条直线上,AB与l2交于点E,则△AED与正方形ABCD的面积之比为
(2012•甘孜州)如图,已知l1∥l2∥l3∥l4,相邻两条平行线间的距离都相等,如果正方形ABCD的四个顶点分别在四条直线上,AB与l2交于点E,则△AED与正方形ABCD的面积之比为 (2013•深圳)如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个顶点分别在这三条平行直线上,则sinα的值是( )
(2013•深圳)如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个顶点分别在这三条平行直线上,则sinα的值是( ) 如图,已知l1∥l2,∠2=30°,∠3=25°,则∠1的度数是( )
如图,已知l1∥l2,∠2=30°,∠3=25°,则∠1的度数是( ) 如图,已知l1∥l2,∠1=65°,∠2=35°,求∠x和∠y的度数.
如图,已知l1∥l2,∠1=65°,∠2=35°,求∠x和∠y的度数.