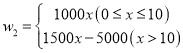题目内容
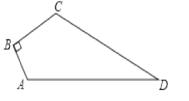
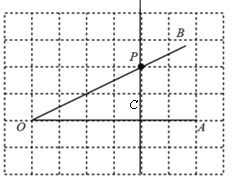
【题目】如图，所有小正方形的边长都为1，点O、P均在格点上，点P是∠AOB 的边 OB 上一点，直线PC⊥OA，垂足为点C.
（1）过点 P 画 OB 的垂线，交OA 于点D；
（2）线段 的长度是点O到直线PD 的距离；
（3）根据所画图形，判断∠OPC ∠PDC（填“＞”，“＜”或“＝”），理由是 ．
【答案】（1）详见解析；（2）OP；（3）＝ ，同角的余角相等
【解析】
（1）过点P作PD⊥OB，交OA于点D即可；（2）根据点到直线距离的定义即可得出结论；（3）根据同角的余角相等即可得出结论．
解：（1）如图即为所求：
（2）∵PD⊥OB
∴线段OP的长度是点O到直线PD 的距离
故答案为：OP
（3）∵PC⊥OA
∴∠PDC+∠CPD=90°
∵PD⊥OB
∴∠OPC+∠CPD=90°
∴∠OPC=∠PDC
故答案为：＝ ，同角的余角相等
练习册系列答案
相关题目
【题目】八年级（1）班张山同学利用所学函数知识，对函数
进行了如下研究：
列表如下：
x | … |
|
|
|
|
| 0 | 1 | 2 | 3 | … |
y | … | 7 | 5 | 3 | m | 1 | n | 1 | 1 | 1 | … |
描点并连线（如下图）
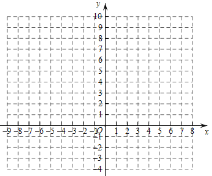
（1）自变量x的取值范围是________；
（2）表格中：
________，
________；
（3）在给出的坐标系中画出函数的图象；
（4）一次函数
的图象与函数的图象交点的坐标为_______.
【题目】为了促进全民健身运动的开展，某市组织了一次足球比赛，下表记录了比赛过程中部分代表队的积分情况.
代表队 | 场次（场） | 胜（场） | 平（场） | 负（场） | 积分（分） |
| 6 | 5 | 1 | 0 | 16 |
| 6 | 6 | 0 | 0 | 18 |
| 6 | 3 | 2 | 1 | 11 |
| 6 | 3 | 1 | 2 | 10 |
（1）本次比赛中，胜一场积______分；
（2）参加此次比赛的
代表队完成10场比赛后，只输了一场，积分是23分，请你求出
代表队胜出的场数.
