题目内容
【题目】已知:如图,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB,AC于点E,F.
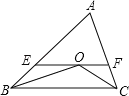
(1)若∠ABC=50°,∠ACB=60°,求∠BOC的度数;
(2)若∠BEF+∠CFE=a,求∠BOC的度数.(用含a的代数式表示)
【答案】(1)125°(2)![]()
【解析】
试题分析:(1)先根据角平分线以及平行线的性质,求得∠EOB与∠FOC,再根据∠EOF=180°求得∠BOC的度数;
(2)先根据角平分线以及平行线的性质,得出∠EOB=∠EBO,∠FOC=∠FCO,再求得∠EOB与∠FOC,再根据∠EOF=180°求得∠BOC的度数.
(1)解:∵BO平分∠ABC
∴∠OBC=![]() ∠ABC
∠ABC
∵∠ABC=50°
∴∠OBC=25°
∵EF∥BC
∴∠EOB=∠OBC=25°
∵CO平分∠ACB
∴∠OCB=![]() ∠ACB
∠ACB
∵∠ACB=60°
∴∠OCB=30°
∵EF∥BC
∴∠FOC=∠OCB=30°
∵EF是一条直线
∴∠EOF=180°
∴∠BOC=125°
(2)∵OB平分∠ABC
∴∠ABO=∠CBO
∵EF∥BC
∴∠EOB=∠OBC
∴∠EOB=∠EBO
同理可得,∠FOC=∠FCO
∴∠EOB=![]() =90°﹣
=90°﹣![]() ∠BEO
∠BEO
∠FOC=![]() =90°﹣
=90°﹣![]() ∠CFO
∠CFO
又∵∠EOF=180°
∴∠BOC=180°﹣∠EOB﹣∠FOC=![]() (∠BEO+∠CFO)=
(∠BEO+∠CFO)=![]()

练习册系列答案
相关题目