题目内容
【题目】小华用两块不全等的等腰直角三角形的三角板摆放图形.

(1)如图①所示两个等腰直角△ABC,△DBE,两直角边交于点F,连接BF、AD,求证:BF=AD;
(2)如果小华将两块三角板△ABC,△DBE如图②所示摆放,使D、B、C三点在一条直线上,AC、DE的延长线相交于点F,过点F作FG∥BC,交直线AE于点G,连接AD,FB,求证:FG=AC+DC;
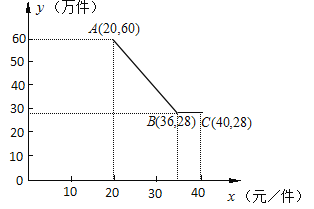
(3)在(2)的条件下,若AG=7![]() ,DC=5,将一个45°角的顶点与点B重合,并绕点B旋转,这个角的两边分别交线段FG于P、Q两点(如图③),若PG=2,求线段FQ的长.
,DC=5,将一个45°角的顶点与点B重合,并绕点B旋转,这个角的两边分别交线段FG于P、Q两点(如图③),若PG=2,求线段FQ的长.
【答案】(1)、证明过程见解析;(2)、证明过程见解析;(3)、![]() .
.
【解析】
试题分析:(1)、根据△ABC,△DBE是等腰直角三角形得到△CDF也是等腰直角三角形,则CD=CF,根据∠BCF=∠ACD=90°,AC=BC得到△BCF≌△ACD,从而得到BF=AD;(2)、根据△ABC、△BDE是等腰直角三角形得出∠ABC=∠BAC=∠BDE=45°即FG∥CD,∠G=45°,则AF=FG,根据CD⊥CF,∠CDF=45°得出CD=CF,则得出答案;(3)、过点B作BH⊥FG垂足为H,过点P作PK⊥AG于点K,根据FG∥BC,C、D、B在一条直线上得出△AFG和△DCF为等腰直角三角形,根据勾股定理得出AF、FG和FD的长度,然后根据题意求出△BQH和△BPK相似,然后求出FQ的长度.
试题解析:(1)、∵△ABC,△DBE是等腰直角三角形, ∴△CDF也是等腰直角三角形;
∴CD=CF, 又∵∠BCF=∠ACD=90°,AC=BC ∴△BCF≌△ACD, ∴BF=AD;
(2)、∵△ABC、△BDE是等腰直角三角形 ∴∠ABC=∠BAC=∠BDE=45°,∵FG∥CD, ∴∠G=45°,
∴AF=FG; ∵CD⊥CF,∠CDF=45°, ∴CD=CF, ∵AF=AC+CF, ∴AF=AC+DC. ∴FG=AC+DC.
(3)、过点B作BH⊥FG垂足为H,过点P作PK⊥AG于点K,
∵FG∥BC,C、D、B在一条直线上, 可证△AFG、△DCF是等腰直角三角形, ∵AG=![]() ,CD=5,
,CD=5,
∴根据勾股定理得:AF=FG=7,FD=![]() , ∴AC=BC=2, ∴BD=3; ∵BH⊥FG,
, ∴AC=BC=2, ∴BD=3; ∵BH⊥FG,
∴BH∥CF,∠BHF=90°, ∵FG∥BC, ∴四边形CFHB是矩形, ∴BH=5,FH=2;
∵FG∥BC, ∴∠G=45°, ∴HG=BH=5,BG=![]() ; ∵PK⊥AG,PG=2, ∴PK=KG=
; ∵PK⊥AG,PG=2, ∴PK=KG=![]() ,
,
∴BK=![]() ﹣
﹣![]() =4
=4![]() ; ∵∠PBQ=45°,∠HGB=45°, ∴∠GBH=45°, ∴∠1=∠2;
; ∵∠PBQ=45°,∠HGB=45°, ∴∠GBH=45°, ∴∠1=∠2;
∵PK⊥AG,BH⊥FG, ∴∠BHQ=∠BKP=90°, ∴△BQH∽△BPK, ∴![]() ,
,
∴QH=![]() ∴
∴![]()

【题目】一空水池现需注满水,水池深 4.9m,现以不变的流量注水,数据如下表所示:
注水时间 t(h) | 0.5 | 1 | 1.5 | 2 |
水的深度 h(m) | 0.7 | 1.4 | 2.1 | 2.8 |
(1)上表反映的变量关系中,注水时间 t 是_____,水的深度 h 是_____.
(2)注满水池需要的时间是_____h.