题目内容
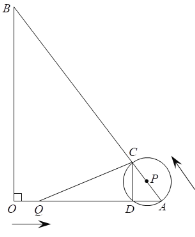
【题目】如图,![]() 是半圆
是半圆![]() 的直径,点
的直径,点![]() 是半圆上的一个动点,
是半圆上的一个动点,![]() 的角平分线交圆弧于点
的角平分线交圆弧于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
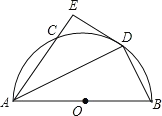
(1)求证:![]() 是半圆
是半圆![]() 的切线;
的切线;
(2)填空:①若![]() ,则
,则![]() __________;
__________;
②连接![]() 、
、![]() ,当
,当![]() 的度数为__________时,四边形
的度数为__________时,四边形![]() 是菱形.
是菱形.
【答案】(1)详见解析;(2)①2;②![]()
【解析】
(1)连接OD,根据角平分线的定义和已知以及平行线的判定得到OD∥AE,即∠ODE=∠E=90,即可证明;
(2)①作DG⊥AB于G,根据相似三角形的面积比等于相似比的平方求出△ADE与△ABD的面积比,根据三角形的面积公式计算即可;②根据菱形的判定定理和等边三角形的性质解答即.
(1)证明:如图1,连接OD
∵AD是∠BAC的角平分线,
∴∠EAD=∠DAB,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠EAD=∠ODA,
∴OD∥AE,![]()
∴∠ODE=∠E=90°
∴![]() 是半圆
是半圆![]() 的切线;
的切线;

(2)①如图2,作DG⊥AB于G
∵AD是∠BAC的角平分线,∠E=90°,DG⊥AB,
∴DE=DG,∠EAD=∠DAB,
∵∠ODE=∠E=90°,
∵△ADE∽△ABD,
∵![]()
∴△ADE与△ABD的面积比为3:4,即
∴AE:AB=3:4;

②如图3,当四边形BDCO是天菱形时,
∴BD=OC=CD=OB,CD∥OB,
当CD∥OB时,BD=AC
∴△AOC为等边三角形
∴当∠BAC=60°时,四边形BDCO是菱形.
故答案为:①3:4;②60°.


【题目】为了解某区初中学生对网络游戏的喜好和作业量多少情况,随机抽取了该区500名同学进行了调查,并将调查的情况进行了整理,如下表:
作业量多少 网络游戏的喜好 | 认为作业多 | 认为作业不多 | 合计 |
喜欢网络游戏 | 180 | 90 | 270 |
不喜欢网络游戏 | 80 | 150 | 230 |
根据抽样调查结果,估计该区12000名初中生“不喜欢网络游戏并认为作业不多”的人数是________.