题目内容
已知三个互不相等的有理数,既可以表示为1,a,a+b的形式,又可以表示0,| b | a |
分析:由于
有意义,则a≠0,则应有a+b=0,则
=-1,故只能b=1,a=-1了,再代入代数式求解.
| b |
| a |
| b |
| a |
解答:解:因为三个互不相等的有理数1,a,a+b分别与0,
,b对应相等,且
为有理数,
∴a≠0,a+b=0,
∴
=-1,b=1,
∴a=-1,
∴a2007a2008=(-1)2007×12008=-1.
| b |
| a |
| b |
| a |
∴a≠0,a+b=0,
∴
| b |
| a |
∴a=-1,
∴a2007a2008=(-1)2007×12008=-1.
点评:本题主要考查了实数的运算,属于探索性题目,关键是根据已知条件求出未知数的值再计算.

练习册系列答案
相关题目
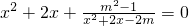 ,其中m为实数,当m为何值时,方程恰有三个互不相等的实数根?求出这三个实数根.
,其中m为实数,当m为何值时,方程恰有三个互不相等的实数根?求出这三个实数根. ,其中m为实数,当m为何值时
,其中m为实数,当m为何值时  ,其中m为实数,当m为何值时,方程恰有三个互不相等的实数根?求出这三个实数根.
,其中m为实数,当m为何值时,方程恰有三个互不相等的实数根?求出这三个实数根.