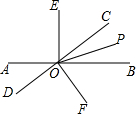
题目内容
如图,O是直线AB上一点,OC为任一条射线,OD平分∠AOC;OE平分∠BOC.
(1)写出图中∠BOD与∠AOE的补角;
(2)如果∠COD=25°,那么∠COE=______;如果∠COD=60°,那么∠COE=______;
(3)试猜想∠COD与∠COE具有怎样的数量关系,并说明理由.
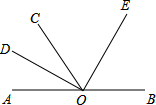
(1)写出图中∠BOD与∠AOE的补角;
(2)如果∠COD=25°,那么∠COE=______;如果∠COD=60°,那么∠COE=______;
(3)试猜想∠COD与∠COE具有怎样的数量关系,并说明理由.

(1)∵OD平分∠AOC;OE平分∠BOC,
∴∠AOD=∠COD,∠BOE=∠COE,
∴∠BOD的补角为∠AOD,∠DOC;∠AOE的补角为∠BOE,∠EOC;
(2)∵∠AOD=∠COD,∠BOE=∠COE,
∴∠DCO+∠COE=
(∠AOC+∠BOC)=
×180°=90°,
∴当∠COD=25°时,∠COE=90°-25°=65°,
当∠COD=60°,∠COE=90°-60°=30°,
故答案为65°;30°;
(3)∠COD+∠COE=90°.理由如下:
因为OD平分∠AOC,OE平分∠BOC.
所以∠COD=
∠AOC,∠COE=
∠BOC.
所以∠COD+∠COE=
∠AOB=
×180°=90°.
∴∠AOD=∠COD,∠BOE=∠COE,
∴∠BOD的补角为∠AOD,∠DOC;∠AOE的补角为∠BOE,∠EOC;
(2)∵∠AOD=∠COD,∠BOE=∠COE,
∴∠DCO+∠COE=
| 1 |
| 2 |
| 1 |
| 2 |
∴当∠COD=25°时,∠COE=90°-25°=65°,
当∠COD=60°,∠COE=90°-60°=30°,
故答案为65°;30°;
(3)∠COD+∠COE=90°.理由如下:
因为OD平分∠AOC,OE平分∠BOC.
所以∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
所以∠COD+∠COE=
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目