题目内容
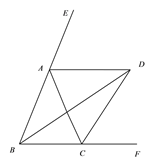
【题目】把多边形的某些边向两方延长,其他各边若不全在延长所得直线的同侧,则把这样的多边形叫做凹多边形.如图①五边形![]() 中,作直线
中,作直线![]() ,则边
,则边![]() 、
、![]() 分别在直线
分别在直线![]() 的两侧,所以五边形
的两侧,所以五边形![]() 就是一个凹五边形.我们简单研究凹多边形的边和角的性质.
就是一个凹五边形.我们简单研究凹多边形的边和角的性质.

(1)如图②,在凹六边形![]() 中,探索
中,探索![]() 与
与![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、之间的关系;
、之间的关系;
(2)如图③,在凹四边形![]() 中,证明
中,证明![]() .
.
【答案】(1)∠BCD=∠A+∠F+∠E+∠ABC+∠EDC-360°;(2)证明见解析.
【解析】试题分析: (1)根据题意结合凸多边形的性质得出540°-(180°-∠BCD)=∠A+∠B+∠D+∠E+∠F,进而得出答案;
(2)利用三角形三边关系,再结合不等式的性质进而得出答案.
试题解析:
(1)连接BD
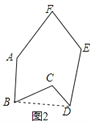
在△BCD中,
∠BCD+∠CBD+∠CDB=180°
又在五边形ABDEF中,
∠A+∠F+∠E+∠ABC+∠EDC+∠CBD+∠CDB=540°
两式相减得
∠BCD=∠A+∠F+∠E+∠ABC+∠EDC-360°
(2)延长BC交AD于点E,
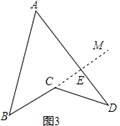
∴AB+AD=AB+AE+ED
在△ABE中 AB+AE>BE
∴AB+AD>BE+ED
又∵BE=BC+CE
在△ECD中,CE+ED>CD
∴BE+ED>BC+CD
∴AB+AD>BC+CD
点睛:此题主要考查了四边形综合以及凸多边形的性质以及凹多边形与凸多边形的性质等知识,正确将凹多边形与凸多边形的关系是解题关键.

练习册系列答案
相关题目