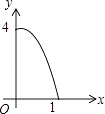题目内容
【题目】解答题
(1)如图1,已知⊙O的半径是4,△ABC内接于⊙O,AC=4 ![]() .
.
①求∠ABC的度数;
②已知AP是⊙O的切线,且AP=4,连接PC.判断直线PC与⊙O的位置关系,并说明理由;
(2)如图2,已知ABCD的顶点A、B、D在⊙O上,顶点C在⊙O内,延长BC交⊙O于点E,连接DE.求证:DE=DC.
【答案】
(1)
解:①连结OA、OC,如图1,

∵OA=OC=4,AC=4 ![]() ,
,
∴OA2+OC2=AC2,
∴△OCA为等腰直角三角形,∠AOC=90°,
∴∠ABC= ![]() ∠AOC=45°;
∠AOC=45°;
②直线PC与⊙O相切.理由如下:
∵AP是⊙O的切线,
∴∠OAP=90°,
而∠AOC=90°,
∴AP∥OC,
而AP=OC=4,
∴四边形APCO为平行四边形,
∵∠AOC=90°,
∴四边形AOCP为矩形,
∴∠PCO=90°,
∴PC⊥OC,
∴PC为⊙O的切线
(2)
证明:∵四边形ABCD为平行四边形,
∴AB∥CD,AD∥BC,
∴∠B+∠A=180°,∠DCE=∠B,
∵∠E+∠A=180°,
∴∠E=∠B,
∴∠DCE=∠E,
∴DC=DE.
【解析】(1)①连结OA、OC,如图1,利用勾股定理的逆定理证明△OCA为等腰直角三角形,∠AOC=90°,然后根据圆周角定理易得∠ABC=45°;
②先根据切线的性质得∠OAP=90°,再证四边形APCO为平行四边形,加上∠AOC=90°,则可判断四边形AOCP为矩形,所以∠PCO=90°,然后根据切线得判断定理得到PC为⊙O的切线;(2)根据平行四边形的性质得AB∥CD,AD∥BC,再由平行线的性质得∠B+∠A=180°,∠DCE=∠B,由圆内接四边形的性质得∠E+∠A=180°,易得∠DCE=∠E,则根据等腰三角形的判定定理即可得到DC=DE.
【考点精析】本题主要考查了平行四边形的性质和切线的性质定理的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.