Question

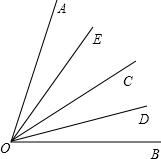已知∠AOB=80°，OC是∠AOB的平分线，OD、OE分别平分∠BOC和∠AOC，
（1）求∠DOE的度数；
（2）当OC在∠AOB内绕O点旋转时，OD、OE仍是∠BOC和∠AOC的平分线，问此时∠DOE的大小是否和（1）中的答案相同？通过此过程，你能总结出怎样的结论？

Answer 1

分析：（1）根据角平分线的定义求得∠AOC=∠BOD=

1

2

∠AOB=

1

2

×80°=40，再由角平分线的定义求得，∠DOC=

1

2

∠BOC=

1

2

×40°=20°，∠EOC=

1

2

∠AOC=

1

2

×40°=20°，即可求解；
（2）根据角平分线的定义求得，∠DOE=∠DOC+∠EOC=

1

2

（∠BOC+∠AOC）=

1

2

∠AOB，从而解决问题．

解答：解：（1）∵OC是∠AOB的平分线
∴∠AOC=∠BOD=

1

2

∠AOB=

1

2

×80°=40°，
∵OD、OE分别平分∠BOC、∠AOC，
∴∠DOC=

1

2

∠BOC=

1

2

×40°=20°∠EOC=

1

2

∠AOC=

1

2

×40°=20°，
∴∠DOE=∠DOC+∠EOC=20°+20°=40°；

（2）当OC旋转时
∵OD、OE仍为∠BOC、∠AOC的平分线，
∴∠DOC=

1

2

∠BOC，∠EOC=

1

2

∠AOC，
∴∠DOE=∠DOC+∠EOC=

1

2

（∠BOC+∠AOC）=

1

2

∠AOB=

1

2

×80°=40°，
∴∠DOE大小不变，
得出结论：OC不论怎样变化，只要∠AOB不变，总有∠DOE=∠AOB．

点评：主要考查了角平分线定义的应用，以及学生解决问题的能力．