题目内容
直角三角形两直角边长分别为3和4,则它斜边上的高是
- A.3.5
- B.2.4
- C.1.2
- D.5
B
分析:依题意作图,如下图所示:根据题意可证△BDC∽△BCA,所以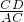 =
=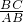 ,由于AC、BC的值已知,所以只需求出AB的值即可求出斜边上的高CD的值,在直角△ABC,可求出斜边AB的值,进而求出CD的值.
,由于AC、BC的值已知,所以只需求出AB的值即可求出斜边上的高CD的值,在直角△ABC,可求出斜边AB的值,进而求出CD的值.
解答: 解:如下图所示:△ABC中,∠C=90°,CD是斜边AB上的高,AC=4,BC=3
解:如下图所示:△ABC中,∠C=90°,CD是斜边AB上的高,AC=4,BC=3
在Rt△ABC中,由勾股定理得:
AB=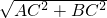 =
=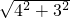 =5,
=5,
∵∠C=∠CDB=90°,∠B=∠B,
∴△BDC∽△BCA,
∴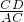 =
=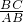
即:CD=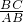 ×AC=
×AC= ×4=2.4.
×4=2.4.
所以,本题应选择B.
点评:本题主要考查直角三角形的性质,关键考查了勾股定理,解题中间运用了相似三角形的判定和性质.
分析:依题意作图,如下图所示:根据题意可证△BDC∽△BCA,所以
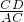 =
=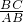 ,由于AC、BC的值已知,所以只需求出AB的值即可求出斜边上的高CD的值,在直角△ABC,可求出斜边AB的值,进而求出CD的值.
,由于AC、BC的值已知,所以只需求出AB的值即可求出斜边上的高CD的值,在直角△ABC,可求出斜边AB的值,进而求出CD的值.解答:
 解:如下图所示:△ABC中,∠C=90°,CD是斜边AB上的高,AC=4,BC=3
解:如下图所示:△ABC中,∠C=90°,CD是斜边AB上的高,AC=4,BC=3在Rt△ABC中,由勾股定理得:
AB=
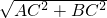 =
=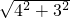 =5,
=5,∵∠C=∠CDB=90°,∠B=∠B,
∴△BDC∽△BCA,
∴
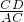 =
=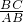
即:CD=
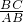 ×AC=
×AC= ×4=2.4.
×4=2.4.所以,本题应选择B.
点评:本题主要考查直角三角形的性质,关键考查了勾股定理,解题中间运用了相似三角形的判定和性质.

练习册系列答案
相关题目