题目内容
【题目】如图,已知正方形ABCD的对角线AC,BD交于点O,点E,F分别是OB,OC上的动点.当动点E,F满足BE=CF时.
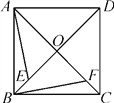
(1)写出所有以点E或F为顶点的全等三角形;(不得添加辅助线)
(2)求证:AE⊥BF.
【答案】(1) △ABE≌△BCF,△AOE≌△BOF,△ADE≌△BAF;(2)见解析
【解析】试题分析:
(1)由已知条件易得AB=BC,∠ABE=∠CBF=45°,结合BE=CF可得△ABE≌△BCF;由此可得∠AEB=∠CFB,从而可得∠AEO=∠BFO,结合∠AOE=∠BOF=90°及OA=OB可得△AOE≌△BOF;由∠ADE=∠BAF=45°,∠AED=∠BFA结合AD=AB即可得到△ADE≌△BAF;
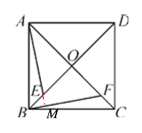
(2)延长AE交BF于点M,由△ABE≌△BCF,可得∠BAE=∠CBF,结合∠CBF+∠ABF=90°可得∠BAE+∠ABM=90°,从而可得∠AMB=90°,由此即可得到AE⊥BF.
试题解析:
(1)由题意可得:
图中以点E或F为顶点的全等三角形有:△ABE≌△BCF,△AOE≌△BOF,△ADE≌△BAF;
(2)延长AE交BF于点M,
∵△ABE≌△BCF,
∴∠BAE=∠CBF,
∵∠CBF+∠ABF=90°,
∴∠BAE+∠ABF=90°,
∴∠AMB=90°,
∴AE⊥BF.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某班10名学生的校服尺寸与对应人数如表所示:
尺寸(cm) | 160 | 165 | 170 | 175 | 180 |
学生人数(人) | 1 | 3 | 2 | 2 | 2 |
则这10名学生校服尺寸的众数和中位数分别为( )
A.165cm,165cm
B.165cm,170cm
C.170cm,165cm
D.170cm,170cm
【题目】下表中有两种移动电话计费方式.
月使用费 | 主叫限定时间 | 主叫超时费 | 被叫 | |
方式一 | 49 | 100 |
| 免费 |
方式二 | 69 | 150 |
| 免费 |
设一个月内主叫通话为t分钟![]() 是正整数
是正整数![]() .
.
![]() 当
当![]() 时,按方式一计费为______元;按方式二计费为______元;
时,按方式一计费为______元;按方式二计费为______元;
![]() 当
当![]() 时,是否存在某一时间t,使两种计费方式相等,若存在,请求出对应t的值,若不存在,请说明理由;
时,是否存在某一时间t,使两种计费方式相等,若存在,请求出对应t的值,若不存在,请说明理由;
![]() 当
当![]() 时,请直接写出省钱的计费方式?
时,请直接写出省钱的计费方式?



