题目内容
如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.
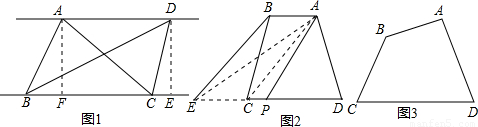
(1)三角形有 条面积等分线,平行四边形有 条面积等分线;
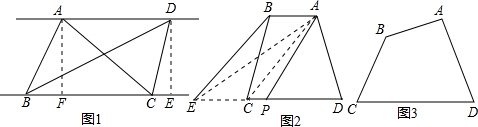
(2)如图①所示,在矩形中剪去一个小正方形,请画出这个图形的一条面积等分线;
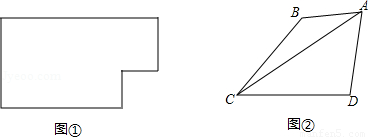
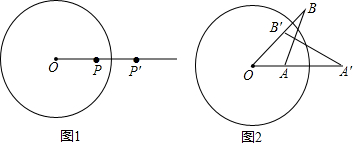
(3)如图②,四边形ABCD中,AB与CD不平行,AB≠CD,且S△ABC<S△ACD,过点A画出四边形ABCD的面积等分线,并写出理由.
【答案】
(1)6;无数(2)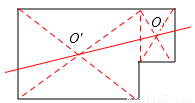 (3)
(3) 理由见解析
理由见解析
【解析】解:(1)6;无数。
(2)这个图形的一条面积等分线如图:

连接2个矩形的对角线的交点的直线即把这个图形分成2个相等的部分.即OO′为这个图形的一条面积等分线。
(3)四边形ABCD的面积等分线如图所示:

理由如下:
过点B作BE∥AC交DC的延长线于点E,连接AE。
∵BE∥AC,∴△ABC和△AEC的公共边AC上的高也相等,∴ S△ABC=S△AEC。
∴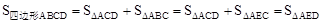 。
。
∵S△ACD>S△ABC,
∴面积等分线必与CD相交,取DE中点F,则直线AF即为要求作的四边形ABCD的面积等分线。
(1)读懂面积等分线的定义,不难得出:三角形的面积等分线是三角形的中线所在的直线;过两条对角线的交点的直线都可以把平行四边形的面积分成2个相等的部分;从而三角形有3条面积等分线,平行四边形有无数条面积等分线。
(2)由(1)知,矩形的一条对角线所在的直线就是矩形的一条面积等分线;
(3)过点B作BE∥AC交DC的延长线于点E,连接AE.根据△ABC和△AEC的公共边AC上的高也相等推知S△ABC=S△AEC;由“割补法”可以求得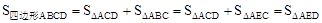 。
。

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
 ×BC×AF,S△BCD=
×BC×AF,S△BCD=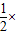 BC×DE
BC×DE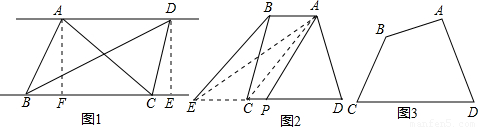
 ×BC×AF,S△BCD=
×BC×AF,S△BCD=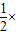 BC×DE
BC×DE