题目内容
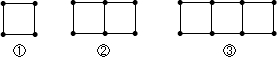
用火柴棒按如图的方式搭三角形.

(1)第⑤号图中的火柴棒根数为
(2)第n号图中的火柴棒根数为
(3)2011根火柴棒全部用完,可以摆多少个这样的三角形?

(1)第⑤号图中的火柴棒根数为
11
11
根;(2)第n号图中的火柴棒根数为
(2n+1)
(2n+1)
根;(3)2011根火柴棒全部用完,可以摆多少个这样的三角形?
分析:(1)可直接数出第⑤号图中的火柴棒根数;
(2)观察图形得到第①号图中的火柴棒根数为3根;第②号图中的火柴棒根数为(3+2)根;第③号图中的火柴棒根数为(3+2×2)根;…;由此可推出第n号图中的火柴棒根数=3+2×(n-1)=(2n+1)根;
(3)由(2)得到2n+1=2011,然后解方程即可.
(2)观察图形得到第①号图中的火柴棒根数为3根;第②号图中的火柴棒根数为(3+2)根;第③号图中的火柴棒根数为(3+2×2)根;…;由此可推出第n号图中的火柴棒根数=3+2×(n-1)=(2n+1)根;
(3)由(2)得到2n+1=2011,然后解方程即可.
解答:解:(1)第⑤号图中的火柴棒根数为11根;
(2)第①号图中的火柴棒根数为3根;
第②号图中的火柴棒根数为(3+2)根;
第③号图中的火柴棒根数为(3+2×2)根;
第④号图中的火柴棒根数为(3+2×3)根;
第⑤号图中的火柴棒根数为(3+2×4)根;
所以第n号图中的火柴棒根数=3+2×(n-1)=(2n+1)根;
(3)2n+1=2011,
解得n=1005,
所以2011根火柴棒全部用完,可以摆1005个这样的三角形.
故答案为11;(2n+1).
(2)第①号图中的火柴棒根数为3根;
第②号图中的火柴棒根数为(3+2)根;
第③号图中的火柴棒根数为(3+2×2)根;
第④号图中的火柴棒根数为(3+2×3)根;
第⑤号图中的火柴棒根数为(3+2×4)根;
所以第n号图中的火柴棒根数=3+2×(n-1)=(2n+1)根;
(3)2n+1=2011,
解得n=1005,
所以2011根火柴棒全部用完,可以摆1005个这样的三角形.
故答案为11;(2n+1).
点评:本题考查了规律型:图形的变化类:通过从一些特殊的图形变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.

练习册系列答案
相关题目


 用火柴棒按如图的方式搭三角形.当第100个图形时,需要
用火柴棒按如图的方式搭三角形.当第100个图形时,需要