题目内容
直角三角形的两条直角边的长分别为5，12，则斜边上的中线为
- A.
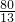cm - B.13cm
- C.6cm
- D.
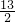cm
D
分析：根据勾股定理求出AB，再根据直角三角形斜边上中线性质求出即可．
解答：
解：由勾股定理得：AB=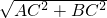
=
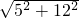=13，
∵CD是直角三角形ACB斜边AB的中线，
∴CD=
AB=，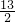
故选D．
点评：本题考查了直角三角形ACB斜边AB的中线和勾股定理的应用，能熟练地运用性质进行推理和计算是解此题的关键，注意：直角三角形斜边上的中线等于斜边的一半．
分析：根据勾股定理求出AB，再根据直角三角形斜边上中线性质求出即可．
解答：
解：由勾股定理得：AB=
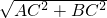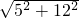==13，∵CD是直角三角形ACB斜边AB的中线，
∴CD=
AB=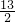，故选D．
点评：本题考查了直角三角形ACB斜边AB的中线和勾股定理的应用，能熟练地运用性质进行推理和计算是解此题的关键，注意：直角三角形斜边上的中线等于斜边的一半．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
