题目内容
【题目】如图，在第1个△A1BC中，∠B=30°，A1B=CB；在边A1B上任取一点D，延长CA1到A2 ， 使A1A2=A1D，得到第2个△A1A2D；在边A2D上任取一点E，延长A1A2到A3 ， 使A2A3=A2E，得到第3个△A2A3E，…按此做法继续下去，则第n个三角形中以An为顶点的底角度数是（ ）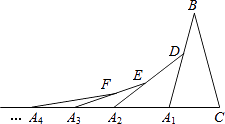
A.（ 
）n75°
B.（ ）n﹣165°
C.（ ）n﹣175°
D.（ ）n85°
【答案】C
【解析】∵在△CBA1中，∠B=30°，A1B=CB，
∴∠BA1C= 
=75°，
∵A1A2=A1D，∠BA1C是△A1A2D的外角，
∴∠DA2A1= 
∠BA1C= ×75°；
同理可得，
∠EA3A2=（ ）2×75°，∠FA4A3=（ ）3×75°，
∴第n个三角形中以An为顶点的底角度数是（ ）n﹣1×75°．
所以答案是：C．
【考点精析】通过灵活运用等腰三角形的性质，掌握等腰三角形的两个底角相等（简称：等边对等角）即可以解答此题．
练习册系列答案
相关题目
